§ 2
与えられたLRC回路のインピーダンスの測定と共振周波数の測定
2-1)実験の原理
本実験では2種類の方法を用いて与えられたLRC回路の共振周波数を求める。
方法 1:インピーダンスを求め、それを用いて共振周波数を求める
「与えられたLRC回路のインピーダンスの測定と共振周波数の測定」(以降、実験g-1と略す)は本方法による。
図 2-
1のような回路で、α、γ間の電圧をVαγとβ、γ間の電圧をVβγとする。
図 2- 1:LRC直列回路
(略 教科書 図13-7参照)
R0:積極的に配置した抵抗、r:導線など、R0以外の回路の抵抗、L:コイルのインダクタンス、C:コンデンサの容量
それぞれの値は Vαγ=V0・sinωt……式< 2- 1>
Vβγ=R0J0・sin(ωt-φ)……式< 2- 2>
と表される。
但し J
:回路電流
J0=V0/Z
ω :交流の各振動数 Z :コイルのインピーダンス
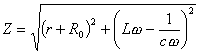
t :時刻
φ :電流の電圧を基準とした位相差
また、 J=Vβγ/R0 であるから、2現象オシロスコープを用いて、VαγとVβγとを同時に描かせることで、インピーダンスZを求めることができる。
また、いろいろな周波数
f についてZを求め、Zが最小になる f を探せば、それが共振周波数である。
方法 2:リサージュ図形を利用して位相差を測定し、共振周波数を求める。
「与えられたLRC回路の電圧と電流の位相差と共振周波数の測定」(以降、実験g-2と略す)は本方法による。
オシロスコープの横軸にVαγを、縦軸にVβγを入力すると、図 2- 2のような 1:1 リサージュ図形が画面に映し出される。
図 2- 2: 1:1 リサージュ図形
(略 教科書 図13-9参照)
Yo,Ymについては教科書と同
式< 2- 2>から、 ωt =0 即ち、 式< 2- 1>より Vαγ=0 のとき、Vβγは図 2- 2に示したY0に相当する。
つまり、 Vβγ|t=0=R0J0・sin(ωt-φ)|t=0=ROJ0・sin(-φ)≡Y0 である。
一方、振幅 f は V0=R0J0=Ym より、
|sinφ|=Y0/Ym
と表される。
よって、位相差が求められ、
φ=0 なら、そのときLRC回路は共振状態にある。
2-2)実験装置
実験装置はg-1,g-2で共通である。
◆オシロスコープ HITACHI V-252 20 MHz
◆低周波発振器A KENWOOD FG-275
◆LCR直列回路 〔L=7.17 mH C=9.91 μF R0=9.95
Ω〕
以上の装置を図 2- 3のように配線した。
図 2- 3:装置配線図(略)
2-3)実験方法
<g-1>
準備
( 1)低周波発振器A(以下、発振器と略す)を以下のように設定した。
電源:OFF 周波数:200
Hz 波形選択:正弦波 出力電圧変化つまみ:出力0
( 2)装置を図 2- 3のように接続した。
( 3)オシロスコープを以下のように設定した。
VOLTS/DIV(CH1、CH2共):左いっぱい(赤つまみはCAL)
AC-GND-DC(CH1、CH2共):GND
V MODE:CH2 TIME/DIV:1
ms/DIV(赤つまみはCAL)
LEVEL:0 SOURCE:CH2 SWEEPMODE:AUTO
( 4)オシロスコープの電源をいれた。
( 5)オシロスコープをさらに以下のように設定した。
AC-GND-DC(CH1、CH2共):AC
CH2 VOLTS/DIV:5mV/DIV
( 6)発振器の電源をいれた。
( 7)発振器の出力電圧を徐々に大きくし、オシロスコープの画面で上下均等に2.0 DIV になるようにした。
( 8)オシロスコープのMODEをCH1にし、CH1 VOLTS/DIVの感度を上げ、波形を大きくした。
( 9)オシロスコープのMODEをALTにした。
測定
オシロスコープの画面上でCH1の振幅が常に
2.0 DIV になるように発振器の出力を調整し、複数の周波数についてCH2の振幅を測定した。
<g-2>
準備
( 1)「<g-1>準備」をした。
( 2)CH1の振幅が 3.0 DIV ぐらいになるように、発振器の出力、オシロスコープのVOLTS/DIVを調節した。
( 3)オシロスコープを以下のように設定した。
SOURCE(X
MODE):CH1 MODE(Y MODE):CH1 TIME/DIV:X-Y
測定
複数の周波数について、Y0、Ymを測定した。
2-4)g-1の測定データ
g-1の測定データと、それを元として計算した電流の振幅、インピーダンスは表
2- 1に示すとおりである。なお、R0=9.95 Ω、 Z=V0/J0 である。
表 2- 1:g-1の測定データ ・ 電流の振幅、インピーダンスの計算結果
|
|
|
|
|
|
|
|
|
周波数 |
CH1の振幅 |
CH2の振幅 |
電流の振幅 |
インピーダンス |
|
|
f (Hz) |
V0 (V) |
R0J0 (×10-2 V) |
J0 (×10-3
A) |
Z (Ω) |
|
|
200 |
0.10 |
1.34 |
1.35 |
74 |
|
|
250 |
0.10 |
1.75 |
1.76 |
57 |
|
|
300 |
0.10 |
1.18 |
1.18 |
85 |
|
|
350 |
0.10 |
1.45 |
1.46 |
69 |
|
|
400 |
0.040 |
1.63 |
1.63 |
24 |
|
|
420 |
0.040 |
1.74 |
1.74 |
23 |
|
|
440 |
0.040 |
1.90 |
1.91 |
21 |
|
|
460 |
0.040 |
2.20 |
2.21 |
18 |
|
|
480 |
0.040 |
2.40 |
2.41 |
17 |
|
|
500 |
0.040 |
2.65 |
2.66 |
15 |
|
|
510 |
0.040 |
2.70 |
2.71 |
15 |
|
|
520 |
0.040 |
2.84 |
2.85 |
14 |
|
|
530 |
0.040 |
2.90 |
2.91 |
14 |
|
|
540 |
0.040 |
3.12 |
3.14 |
13 |
|
|
550 |
0.040 |
3.18 |
3.20 |
13 |
|
|
560 |
0.040 |
3.18 |
3.20 |
13 |
|
|
570 |
0.040 |
3.19 |
3.21 |
12 |
|
|
580 |
0.040 |
3.19 |
3.21 |
12 |
|
|
590 |
0.040 |
3.19 |
3.21 |
12 |
|
|
600 |
0.040 |
3.20 |
3.22 |
12 |
|
|
620 |
0.040 |
3.07 |
3.09 |
13 |
|
|
640 |
0.040 |
2.93 |
2.94 |
14 |
|
|
660 |
0.040 |
2.83 |
2.84 |
14 |
|
|
680 |
0.040 |
2.77 |
2.78 |
14 |
|
|
700 |
0.040 |
2.50 |
2.51 |
16 |
|
|
750 |
0.040 |
2.20 |
2.21 |
18 |
|
|
800 |
0.040 |
1.38 |
1.38 |
29 |
|
|
850 |
0.040 |
1.65 |
1.66 |
24 |
|
|
900 |
0.040 |
1.48 |
1.48 |
27 |
|
|
950 |
0.040 |
1.38 |
1.38 |
29 |
|
|
1000 |
0.040 |
1.22 |
1.22 |
33 |
|
|
1100 |
0.040 |
1.05 |
1.06 |
38 |
|
|
1200 |
0.040 |
0.900 |
0.905 |
44 |
|
|
1300 |
0.040 |
0.800 |
0.804 |
50 |
|
|
|
|
|
|
|
2-5)g-1の解析及び結論
表 2- 1のデータから周波数fとインピーダンスZを抜き出し、プロットしたのが、図
2- 4である。
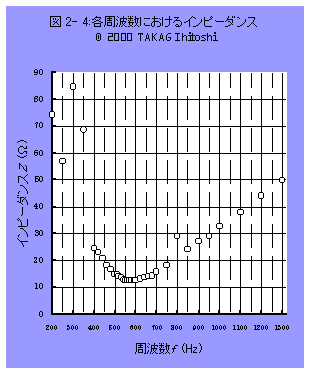
Z が最小であるときの f が共振周波数 f0 だから、結果として、
f0 =590 Hz
が求まる。
2-6)g-2の測定データ
g-1の測定データと、それを元として計算した位相の絶対値|φ|は表
2- 2に示すとおりである。
表 2- 2:測定データ ・ 位相の絶対値の計算結果
|
|
|
|
|
|
|
|
|
周波数f (Hz) |
2Y0
(DIV) |
2Ym
(DIV) |
位相(絶対値)|φ| (rad) |
|
|
|
|
400 |
4.0 |
4.8 |
0.99 |
|
|
|
500 |
3.7 |
6.6 |
0.60 |
|
|
|
520 |
3.0 |
7.0 |
0.44 |
|
|
|
540 |
2.1 |
7.2 |
0.30 |
|
|
|
560 |
1.1 |
7.2 |
0.15 |
|
|
|
580 |
0.0 |
3.7 |
0.00 |
|
|
|
600 |
1.0 |
7.2 |
0.14 |
|
|
|
620 |
1.9 |
7.1 |
0.27 |
|
|
|
700 |
4.0 |
6.3 |
0.69 |
|
|
|
|
|
|
|
2-7)g-2の解析及び結論
表 2- 2のデータから周波数fと位相(絶対値)|φ|を抜き出し、プロットしたのが、図
2- 5である。
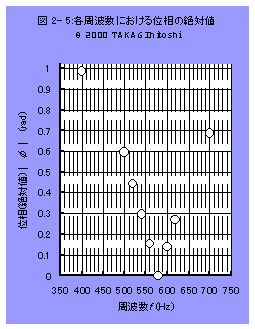
φ=0 で回路は共振しているから、
共振周波数f0 =580 Hz
が求まる。
2-8)検討と考察
g-1、g-2で求められた共振周波数を比較する。差は
10 Hzである。
実験過程及び測定操作において不適切であった点は、思い当たらない。
有効数字は<g-1>:CH1のそれが2桁であったことに起因し、2桁である。
<g-2>:測定データが2桁であったことに起因し、2桁である。
また、実験の妥当性はg-1、g-2全体としては、結果の共振周波数がほぼ同じ値に求まったので、高いと考える。
ただ、g-1について、図 2- 4より f =300,350,800
Hz においてプロットされた点がほかの点から推量される位置から逸脱している。よって、g-1の妥当性はやや低い。
このことについて、原因を考える。図 2- 4からf=300,350,800
Hz の点を除き、近似曲線(:6次の多項式近似)を考えると、
Z= -3.27×10−16 f 6 +1.65×10−12 f 5 -3.10×10−9 f 4 +2.49×10−6 f 3 -4.51×10−4 f 2 -0.372 f +1.51×102……式< 2- 3>となる。式< 2-
3>より、推測される f =300,350 Hz でのインピーダンスZはそれぞれ 44,33 Ω である。これらは測定値より計算された値の1/2に近い。よって、以下の仮説が立てられる。
仮説:f =300,350 HzでのCH2電圧値(R0J0)の測定の際、VOLTS/DIVを正しくは20
mV/DIVのところ、10 mV/DIVと間違えて記録した
なお、f =800 Hzについては、推定インピーダンスZは 21 Ωで、原因は不明である。
誤差の要因は、オシロスコープの画面に現れる線に太さがある程度あることである。
<§ 2 終わり>
Copyright(c) 2000 TAKAGI-1 All rights reserved.