§ 1
CR直列回路の特性時間の測定
1-1)実験の原理
CR直列回路に電圧Eがかかっている場合について考える。ここでコンデンサの容量をC、抵抗の値をRとし、コンデンサと抵抗、それぞれの両端間電圧をVC、VRとする。また、時刻t においてコンデンサに蓄積された電荷をq、回路に流れる電流をiとすると、キルヒホッフの法則より
E=VC+VR=(q/c)+iR
が成立する。dq/dt=i より、
![]() ……式< 1- 1>
……式< 1- 1>
となり、これがCR直列回路の特性を示す微分方程式である。
CR直列回路に、 E= 0(t<0,t1<t〔但し 0<t1〕), E0(0≦t≦t0) の電圧が加わったとき、式< 1- 1>を初期条件:t=0
で q=0 すなわち VC=q/c =0 の下で解くと
VR=iR=E0・exp[-t /(CR)]……式<
1- 2>
となる。本式より、CRはt=0でのVRの値がe−1倍となる時間に相当し、VRの時間変化の測定により、CRの値の算出が可能である。
1-2)実験装置
◆オシロスコープ HITACHI V-252 20MHz
◆低周波発振器A KENWOOD FG-275
◆CR回路 〔R=10.00kΩ〕
以上の装置を図 1- 2のように配線した。
図 1- 2:装置配線図 (略)
1-3)実験方法
( 1)装置を図 1- 2のように配線した。
( 2)オシロスコープを表 1- 1のように設定した。
( 3)低周波発振器Aから山と谷の高さの差が 3 V で 500 Hz の方形波を発振させ、最低電位が 0 V になるように、DC
OFFSETを調節した。
( 4)CH1 AC-GND-DCをGNDにし、電圧値 0 V を画面目盛線の最下横軸に一致させ、その後CH1 AC-GND-DCをDCに戻した。
( 5)TIME/DIVを 50 μs にし、水平POSITIONにより、 t=0 の点を画面左端の縦軸に合わせた。
( 6)画面上でVRの値を t =0~500 μs の範囲で 50 μs ずつ、それぞれの時刻について11点読み取った。
|
表
1- 1:オシロスコープの初期設定 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
CH1
POITION |
中央 |
|
|
|
|
|
|
|
CH2
POITION |
中央 |
|
|
|
|
|
|
|
CH1
VOLT/DIV |
1V(赤つまみはCAL) |
|
|
|
|
|
|
|
CH2
VOLT/DIV |
1V(赤つまみはCAL) |
|
|
|
|
|
|
|
AC-GND-DC |
MODEスイッチでCH1またはCH2に切り替え、それぞれのCHで、AC-GND-DCをGNDにし、 |
||||||
|
|
POSITIONで、OVのレベルをが画面中央にそろえ、その後ともにDCにした。 |
|
|||||
|
MODE |
CH1 |
|
|
|
|
|
|
|
POLARITY |
NORMAL |
|
|
|
|
|
|
|
INTENSITY |
右いっぱい |
|
|
|
|
|
|
|
FOCUS |
中央 |
|
|
|
|
|
|
|
SOURCE1 |
INT |
|
|
|
|
|
|
|
SOURCE2 |
CH1 |
|
|
|
|
|
|
|
SWEEPMODE |
AUTO |
|
|
|
|
|
|
|
LEVEL |
中央(0) |
|
|
|
|
|
|
|
TIME/DIV |
1ms(赤つまみはCAL) |
|
|
|
|
|
|
|
水平POSITION |
中央 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1-4)測定データ
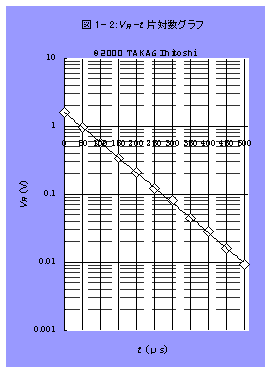
測定により得られたデータは表 1- 2のとおりである。表
1- 2のデータを片対数グラフにしたのが、図 1- 2である。
|
表
1- 2:測定データ |
|
|
|
|
|
|
|
|
|
|
|
|
|
t (μs) |
VR
(V) |
|
|
|
|
0 |
|
1.56 |
|
|
|
50 |
|
0.94 |
|
|
|
100 |
|
0.56 |
|
|
|
150 |
|
0.34 |
|
|
|
200 |
|
0.21 |
|
|
|
250 |
|
0.12 |
|
|
|
300 |
|
0.080 |
|
|
|
350 |
|
0.044 |
|
|
|
400 |
|
0.028 |
|
|
|
450 |
|
0.016 |
|
|
|
500 |
|
0.0092 |
1-5)解析及び結論
式< 1- 2>の10を底とする常用対数をとると log10VR=log10E0-t(log10e)/(CR)
となる(但し、ここでの t の単位はs(:秒)である)。図 1- 2でプロットした点は、ほぼ直線上に並んでいる。よって、実験値が理論値から逸脱していないことが確認できる。
ここで、図 1- 2上の点を結ぶ最小二乗線を最小二乗法でもとめると、
log10VR=a+b・t (a=0.20±0.01 b=-4.4×10−3)〔VR(V) t(μs)〕
となる。同線を図 1- 2にひく。
したがって log10e/(CR)=4.4×103 であるから、 CR=9.8×10−5
F・Ω である。
R=1.000×104 Ωだから、結論として、
C=9.8×10−9 F
と求められた。
1-6)検討と考察
実験過程及び測定操作において不適切であった点は、思い当たらない。
有効数字は測定データのそれが2桁であったことに起因し、2桁である。
図 1- 2でプロットした点の分布状況を相関係数で表すと
rxy=-1.0 であるので、実験の妥当性は極めて高いと考える。
誤差の要因は、VRの値が小さくなるほど、VOLTS/DIVを小さくするため、オシロスコープの画面に現れる線がぼやけることである。
<§ 1 終わり>
Copyright(c) 2000 TAKAGI-1 All rights reserved.