↑クリックで拡大
高木 一 (TAKAGI, Hitoshi)
公開開始 2024/ 5/ 2
会話コーパス※とレーベンシュタイン距離※※を用いて、新たな問いかけ文に対して、複数の応答文候補の中から適切な応答文を選択する能力を高められることを確認しました。
例えば、下記のケース例で示す AさんとBさんの会話で、Bさんの応答文が(1)〜(5)の中で(1)であることを、計算で推定することが可能です。 それぞれ選択肢が5つの25,000余のケースについて推定を実施した結果、平均正答率は、23.7%で、ランダムに選択した場合の正答率である 20%の1.19倍でした。ランダム選択による正答率より高い正答率になる確率は、統計的な検定の結果、90%以上です(つまり、有意水準0.1において、ランダム選択による正答率より高い正答率になると言えます)。※※※
ケース例
Aさん: そうなんだ。あ、でもそれ植物油、植物。
Bさん:註
※コーパス (corpus)。自然言語の文章や使い方を大規模に収集し、コンピュータで検索できるよう整理されたデータベースのこと(コーパスとは?基本的な意味からAIへの活用についても解説 | DXを推進するAIポータルメディア「AIsmiley」)。
※※レーベンシュタイン距離 (Levenshtein distance)。2つの文字列がどの程度異なっているかを示す距離の一種(レーベンシュタイン距離 - Wikipedia 2023年3月26日 (日) 01:19の版)。
※※※本確率は、下記する計算方法をした場合の値です。今後、計算方法の改良により、向上できると考えます。
下記の計算方法(アルゴリズム)で推定しました。
凡例:
評価対象の会話「Ea」---「Eb」。Ebの候補として、Ebc[j] (j=0,1,2,…)があると仮定。
計算に使用する会話データ「La[k]」---「Lb[k]」(k=0,1,2,…)。
Length(str): 文字列strの長さ。
Length(M): 配列Mの要素の個数。
(1) EaとLa[k]の間のレーベンシュタイン距離を計算する。文字列str1とstr2のレーベンシュタイン距離をLD(str1, str2)と表す。すべてのLa[k]について、それぞれ 正規化されたレーベンシュタイン距離 NormalizedLD(Ea, La[k]) を計算する。
NormalizedLD(Ea, La[k])=LD(Ea, La[k])/max(Length(Ea), Length(La[k])) .
(2) NormalizedLD(Ea, La[k])が最小なk を10個+α探し出す(同じ値である場合は全て採用する)。探し出されたkをK[n] (n=0,1,2,…)と表記する。
3-1) すべてのK[n]について、それぞれ NormalizedLD(Ebc[j], Lb[K[n]])=LD(Ebc[j], Lb[K[n]])/max(Length(Ea), Length(Ln[K[n]])) を計算する。
Kに関する平均値 AvrNormalizedLD(j, 0)=(1/Length(n))×Σ(n=0,1,2,…) NormalizedLD(Ebc[j], Lb[K[n]]) を計算する (Σは、総和記号)。
3-2) 同様に、
AvrNormalizedLD(j, +2)=(1/Length(K))×Σ(n=0,1,2,…) NormalizedLD(Ebc[j], Lb[K[n]+2]) 、
AvrNormalizedLD(j, +1)=(1/Length(K))×Σ(n=0,1,2,…) NormalizedLD(Ebc[j], Lb[K[n]+1]) 、
AvrNormalizedLD(j, -1)=(1/Length(K))×Σ(n=0,1,2,…) NormalizedLD(Ebc[j], Lb[K[n]-1])
を計算する。なお、上記3式での Lb[K[n] +2, +1 or -1] は略記であり、正確には Lb[(K[n] +2, +1 or -1 + Length(Lb))%Length(Lb)] である(%は剰余演算子(割り算の余り))。
3-3) Fit(j)=( AvrNormalizedLD(j, +2) - AvrNormalizedLD(j, 0) + AvrNormalizedLD(j, +1) - AvrNormalizedLD(j, 0))5×(1-AvrNormalizedLD(j, -1)) を計算する。
(4) 評価値 Fit(j)が最大となるEbc[j]が、Eaの応答文として最適である。
適切な応答文を選択する選択能力を測定するためのテスト計算を実施して、2節に記した方法による選択能力を評価しました。
「名大会話コーパス※」内の会話(Aさん「a」---Bさん「b」)のうち、応答者(Bさん)が10〜30歳代女性であるもの。なお、順序は、同コーパス収録の順序です。自然な会話文では表れないコーパス内での特別な表記(例: 相槌を表す括弧書き、プライバシー情報を表す伏字や記号)は、表記箇所、又は文単位での削除をしました。
上記の会話文(「a」---「b」の組) 43,406件(indexが 0〜43405)を、43,106件と300件に分けて、
前者を計算に使用する会話データ「La[k]」---「Lb[k]」(k=0,1,2,…)、
後者をテスト評価対象の会話データ「Ea[i]」---「Eb0[i]」(i=0,1,2,…)にします。
※ 藤村逸子・大曽美恵子・大島ディヴィッド義和、2011「会話コーパスの構築によるコミュニケーション研究」藤村逸子、滝沢直宏編『言語研究の技法:データの収集と分析』p. 43-72、ひつじ書房.
下記の仕様でテスト計算を実施しました。
10 RUN×300ケース/RUN = 総 3000ケース
比較用の誤りの応答文は、テスト評価対象の会話データの中で、正しい応答文のindexを+10, +20, +30, +40して作成。(正答1ケ、誤答4ケの 5択)
各RUNの条件と結果を下表に示します。
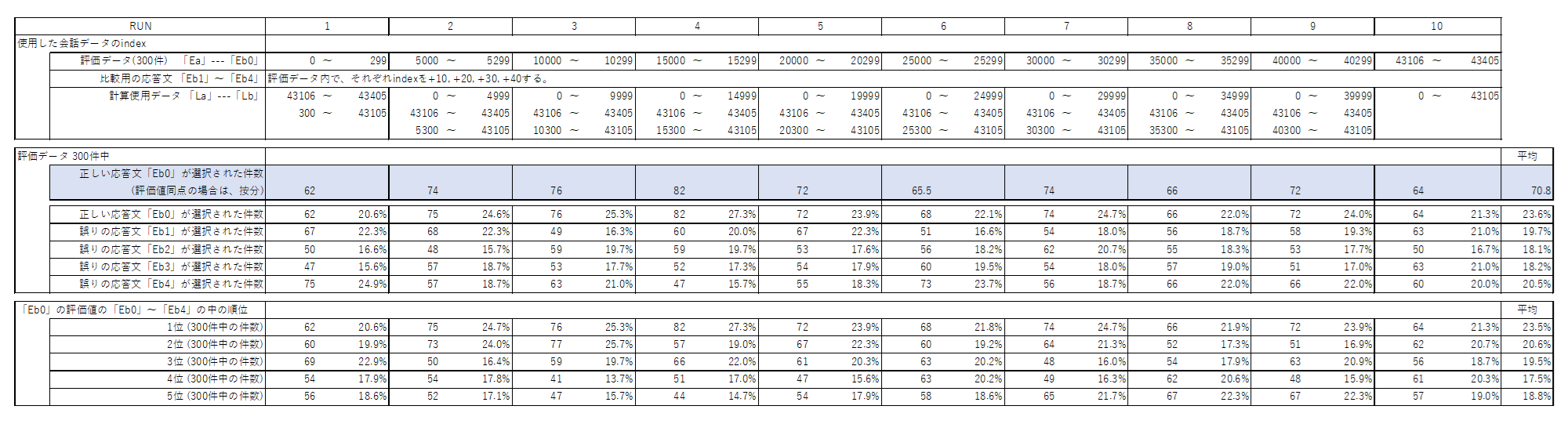
表1.テスト計算1の各RUNの条件、及び結果

↑クリックで拡大
平均の正答数は、300ケース中 σ= 70.8ケース。標準偏差 s= 6.24ケースでした。
正しい応答文が選ばれた確率は、23.6%、比較用の誤りの応答文が選ばれた確率は、18.1〜20.5%でした。
下記の仕様でテスト計算を実施しました。
10 RUN×300ケース/RUN = 総 3000ケース
比較用の誤りの応答文は、テスト評価対象の会話データの中で、indexをランダムに4件 選んで(ただし、正しい応答文とは重複しない)作成。(正答1ケ、誤答4ケの 5択)
各RUNの条件と結果を下表に示します。
表2.テスト計算2の各RUNの条件、及び結果

↑クリックで拡大
平均の正答数は、300ケース中 σ= 72.3ケース。標準偏差 s= 6.96ケースでした。
正しい応答文が選ばれた確率は、24.0%、比較用の誤りの応答文が選ばれた確率は、17.9〜20.2%でした。
テスト計算1の結果とよく合っており、
テスト計算1で実施した比較用の誤りの応答文の作成方法(テスト評価対象の会話データの中で、正しい応答文のindexを+10, +20, +30, +40して作成)と、
テスト計算2で実施した比較用の誤りの応答文の作成方法(テスト評価対象の会話データの中で、indexをランダムに4件 選んで(ただし、正しい応答文とは重複しない)作成)
の結果が、ほぼ一致することが分かります。
テスト計算1及び2よりも多くのケース数でテスト計算を実施し、本方法による選択能力を評価しました。
下記の仕様でテスト計算を実施しました。
86 RUN×300ケース/RUN = 総 25800ケース
比較用の誤りの応答文は、テスト評価対象の会話データの中で、indexをランダムに4件 選んで(ただし、正しい応答文とは重複しない)作成。(正答1ケ、誤答4ケの 5択)
各RUN(全 86 RUN)それぞれ 300ケース中の正答数の結果を、ヒストグラムにして下図に示します。

図1. テスト計算3での正答数の分布 縦軸: RUN数。横軸: 正答数("(p,q]"は"p超えq以下"の意味)
平均の正答数は、300ケース中 σ= 71.2ケースでした。平均正答率は、23.7%です。5択からの選択であるため、ランダムに選択した場合の正答率は 20%ですが、その1.19倍でした。
標準偏差 s= 8.37ケースでした。
ランダム選択での平均正答数は、300ケース中 60ケースですが、60=σ-1.34s であるため、正答数が正規分布していると仮定すると、本方法による選択の正答率がランダム選択による正答率(即ち、正答数 60ケース)より大きい確率は、91.0%です。
【2024/5/7追記】より正確に、t分布(自由度 86)で考えると、本方法による選択の正答率がランダム選択による正答率(即ち、正答数 60ケース)より大きい確率は、90.8%です。
なお、正答数が 60ケースより大きいRUNは、全 86 RUN中 78 RUN (90.7%)でした。
したがって、ランダム選択による正答率より高い正答率になる確率は、統計的な検定の結果、90%以上です(つまり、有意水準0.1において、ランダム選択による正答率より高い正答率になると言えます)。
公開開始: 2024/ 5/ 2
© 2024 TAKAGI-1