| 最終残りカード数 | 0 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 | 26 | 28 | 30 | 32 | 34 | 36 | 38 | 40 | 42 | 44 | 46 | 48 | 50 | 52 | 計 |
| 度数 | 8 | 0 | 7 | 0 | 0 | 2 | 1 | 1 | 2 | 2 | 5 | 5 | 6 | 3 | 5 | 3 | 3 | 6 | 6 | 1 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 68 |
 |
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
最終内容更新08/ 5/25 最終編集校正--/--/--
関連: 統計学リンク プログラミング関連リンク
カードゲームをシミュレートするプログラムを作成し、その計算結果とカードゲームを実際に行った実験結果を、統計的に比較した。プログラムが本当にカードゲームをシミュレートできているかに関して、結論は出なかった。
私は、2001年夏、計算機数学(2001年度前期工学部専門科目)の課題において、4本のプログラムを書いたが、そのうちの1本について、計算結果に疑問が生じた。同じ講義をとっている友達とメールで計算結果の「答え合わせ」をしたのだが、それが微妙に異なるのだ。
そのプログラムは以下の問題を解くためのものであった。
＞課題２（石原）
一人トランプ「カップル」の成功確率は
ソリティアと呼ばれるトランプの一人遊びには色々な種類がある。 比較的単純なカップルというトランプゲームで最後に残る枚数の期待値はどの程度か。ヒストグラムを求めて成功する確率、期待値、標準偏差を求めなさい。 カップルは下図のように左から右、上から下へと4枚ずつカードを並べていき、その途中、縦、横、斜め、に数字が会えば（図１）その２枚を取り除き、順に詰めていき（図２）、カードを追加して並べていくゲームです。
＊各図は略
私はプログラムを書くと同時に、検定のため、実験を行った(繰り返し「カップル」を行った)。そして得た結果とも、計算結果が微妙に違う。この微妙な違いが、心配症ゆえなのか、それともプログラムに問題があるのかが気になっていた。
ということで、統計学的な検定を行う。
まず、実験によって得た最終カード数の分布を示す。なお、普通に「カップル」を行うときは、カードを取り除く順番をいろいろ考えて、残りカード数をできるだけ少なくしようとするが、ここでは、プログラムと同じアルゴリズムで(少なくともプログラマーたる私が、プログラムに組み込んだ、と思っているアルゴリズムで)、即ち機械的にカードを取り除いた。
実験の度数分布
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
つぎにプログラムを走らせ得た度数分布をヒストグラムとしたものを示す。横軸が最終残りカード数、縦軸が度数である。なお、総試行回数は1,000,000回(百万回)である。
計算結果の度数分布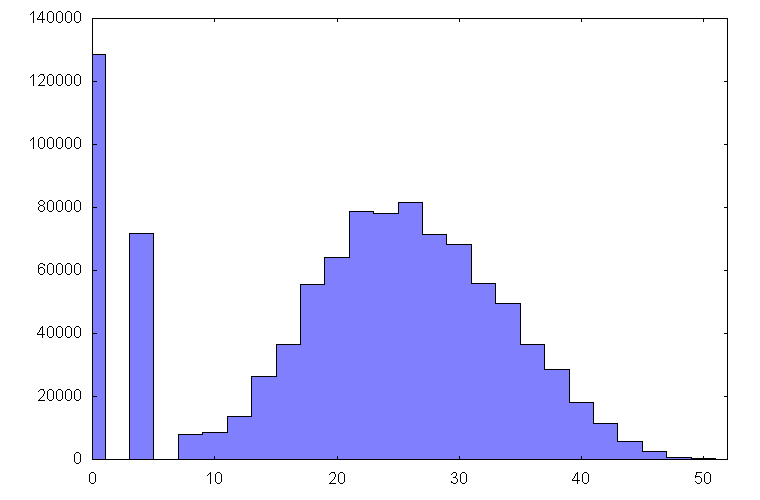
両者の統計的情報を計算する。
実験結果と計算結果の統計的情報
| 実験 | 計算 | |
| 試行回数 | 68 | 1,000,000 |
| 成功確率 | 0.117647 | 0.128468 |
| 平均最終残りカード数 | 21.1471 | 21.0946 |
| 標本標準偏差 | ----- | 11.9990 |
| 不偏標本標準偏差 | 12.4316 | ----- |
計算による試行回数は極めて多いので、その不偏標本標準偏差をもって、計算の母標準偏差としてもよい、と考える。
(標本分散)×(試行回数)=(不偏標本分散)×[(試行回数)-1] より、
メモ: (分散)=(標準偏差)2
(計算の母分散) = (計算の不偏標本分散) = 11.9990 2 × 1000000 / (1000000- 1) = 143.9761
また、上と同じ理由により、よって、計算の母分布に関するデータがそろった。
プログラムが全く正しいと仮定すると、「カップル」の母分布とこの計算の母分布が一致するので、計算の母分布(=「カップル」の母分布,if プログラムが正しい)と実験データ(「カップル」の母集合から無作為抽出されたデータ)を対照させることにより、プログラムの正当性が分かる。
今一度、整理しておこう。
「カップル」の標本と母集合
| 標本 | 母集合 | |
| 試行回数 | 68 | ∞ |
| 成功確率 | 0.117647 | 0.128468 |
| 平均 | 21.1471 | 21.0946 |
| 不偏標本標準偏差 母分散 | 12.4316 ----- | ----- 143.9761 |
まず、これから複雑な式を扱う事になるので、各数値に文字をあてる。
文字の説明
| 「カップル」の標本と母集合 | 標本 | 母集合 |
| 試行回数 | n 68 | ∞ |
| 成功確率 | p 0sample 0.117647 | p 0 0.128468 |
| 平均 |  21.1471 | μ 21.0946 |
| 不偏標本標準偏差 母分散 |  12.4316----- | ----- σ2 143.9761 |
英小文字は実現値を表している。以降、
など、英大文字となっているものが登場するが、それは、対応する英小文字と同じものを一般的に表している。深刻に考える必要はないと思う
すぐで申し訳ないが、以下の「↓ここから」から「↑ここまで」の間、上で決めた文字を一部忘れてほしい。この間の p は、上のp 0に相当し、は、上のp 0sample の一般値に相当する。
↓ここから
母比率の推定:
ある性質をもつ…X = 1 (確率 p )、もたない…X = 0 (確率 1-p )とすると、
Y = nnが大ならば、
は近似的に標準正規分布N(0,1)に従う。
信頼水準 γ として、
。
ただし、z1は、N(0,1)において、確率 P{ -z1 < X < z1 } = γ。↑ここまで
より、
∴ z1 = 0.276956
αを下図のように定める。
表計算ソフトやcgiでαを計算すると、α = 1 - 0.781814 = 0.218186 = 21.8186 ％ となる。なお、z1(の絶対値)がこれより大きい値をとる確率は、0.781814 である。
これをよく行う統計的仮説検定の目から見てみる。
帰無仮説 H0: プログラムは正しくない
対立仮説 H1: プログラムは正しい
とする。すると、以下のようになる。
統計的仮説検定
| 有意水準(:危険率) | H0 |
| 1% | 採択 |
| 5% | 採択 |
| 10% | 採択 |
| 20% | 採択 |
| 21.8186% | |
| 25% | 棄却:プログラムは正しい |
有意水準25%って、みた事ない... 通常は1%,5%が使われる
なお、H0 が採択されたからといって、プログラムが正しくない事を示しているのではない。
上と同じ方法で、各残りカード数の確率について検定する。結果はこちら。
αが小さいことが、プログラムが正しい事を表している。
正規分布にしたがわない分布の平均について検定する方法を少なくとも私は知らない。すいません
正規分布にしたがわない分布の分散・標準偏差について検定する方法を少なくとも私は知らない。すいません。このことが分かったんで、4.1.1節を急遽書いたわけです。
まったく誤っているとはいえないし、まったく正しいともいえない、これ以上のことは云えない。
以上
©2002,2008 TAKAGI-1
本ページの公開が開始された 2002/ 3/ 9は、京大経済学部の入試合格発表日(平成14年度入学)でした。H君、合格おめでとう。