�u�M�d�q���o�Ɋւ�������v���|�[�gWeb��
![]()
1)�����ړI
�M�d�q���o���ۂɔ��������ߒ����ɐ^��ǂ��g���Ē��ׂ餑��� Richardson-Dushmanv �̎��� Child-Langmuir �̎��������ɂ���Ċm���ߤ�����Ƀt�B�������g�̍ޗ��ł���^���O�X�e���̎d���������ߤ����Ɍ������v��p���t�B�������g�̉��x�𑪒肷�邱�Ƃɂ��Planck�̍����t�˂̌����Ɋ�Â��������̂̔�ڐG�^���x����ɂ��Ă̔F���邱�Ƃ��{�����̖ړI�ł���
2)�����̌���
�������d�q�ɂ��ĤFermi-Dirac�̕��z���Ă͂߂�Ƥ�����\�ʂ���P�ʖʐϤ�P�ʎ��ԓ������яo���d�q�̐�(�M�d�q���o�d�����x)j����
<Richardson-Dushman�̎��c�c[ 1]>
![]()
�A����s:��Ή��x ��:�d����
�`=4��mek�Q/h�R=1.20�~10�UA�m�|�Q�K�|�Q
m:�d�q�̎��� e:�f�d��
k:�{���c�}���萔 h:�v�����N�萔
�ŕ\�����
��ɐ^��ǂ̔M�d�q���o���ۂɂ͉��x������ԂƋ�ԓd�א�����Ԃ����݂��顑O�҂ɂ����Ĥ�M�d�q�͂��ׂėz�ɂɗ��ꍞ�ނ��ߓd����[ 1]���ɏ]�����Ή��x�݂̂̊��ƂȂ顈�����҂ł͋�ԓd�ׂ̂��߂ɔM�d������������邽�߈��l�ȏ�͓d��������Ȃ������ēd����[
1]���ɏ]��Ȃ���A�ɋy�їz�ɂ����S�~���ɂȂ��Ă���ꍇ�̒P�ʖʐϓ�����̋�ԓd�א����d��j �͎����ɏ]���
<Child-Langmuir�̎�(3/2��@��)�c�c[ 2]>
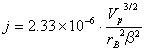 (A/m�Q)
(A/m�Q)
�A���r�a:�z�ɔ��a
��:r�a/r��(r��:�A�ɔ��a)�̊�
(�A���r�a/r��>10�̂Ƃ����`1)
����Ĥ����J�\�[�h���x��������̃J�\�[�h�d���ɑ���z�ɓd�����Ⴂ�Ԃ͋�ԓd�א�����ԂŤ[ 1]���ɏ]����d�����㏸����ɂ꤉��x������ԂɈڂ褈ȍ~��[ 2]���ɏ]���A�ɂ̉��x�ɂ���Č��܂���̉��x�����d���������
�܂���A�ɉ��x�������Ȃ�ߒ�������J�\�[�h�d���������Ă����ߒ��ɂ����Ăͤ�P�ʎ��ԓ�����̔M�d�q���o�ʂ����債�����ċ�ԓd�א�����Ԃ�艷�x������ԂɈڂ�z�ɓd�����������ɍ����Ȃ�
3)�������u
�{�����ł͈ȉ��̑��u���g�p�����
(1)��d���d�� KIKUSUI ELECTRONICS CORP�� 7372A
(2)��d���d�� KIKUSUI ELECTRONICS CORP�� 7318A
(3)�~���A���y�A�v YOKOGAWA ELECTRIC WORKS LTD.��
(4)�d���v YOKOGAWA ELECTRIC WORKS LTD.��
(5)�d���v YOKOGAWA ELECTRIC WORKS LTD.��
(6)���[�h��
(7)�������v CHINO PYROSTAR MODEC IR-U
(8)�M�d�q���o��Ɋ�
�܂����L�̑��u���ȉ��̔z���}�̂Ƃ���ɐڑ������
�} 1:�z���}
P�P:��d���d��(0~300V) P�Q:��d���d��(0~4.5A)
mA:�~���A���y�A�v A:�d���v V:�d���v �@(��)
4)�������@
(1)�J�\�[�h�ɗ����d��I ��3.8A,3.9A,4.0A,4.1A,4.2A�ƕς�����ꂼ��̓d���l�ɑ���z�ɓd��V����0V����200V�܂ŏ����ς��Ă�������̂Ƃ��̓d����y�їz�ɓd��J���𑪂����
(2)V��=0�ŃJ�\�[�h�d��I��2.6A����4.4A�܂�0.2A���݂ŕς�����ꂼ��̃t�B�������g���x���������v�ŕ����肵���
5)����f�[�^
�������@(2)�œ���ꂽ�f�[�^�͕\ 1�̂Ƃ���ł��顕\ 1�̃J�\�[�h�d���Ƥ�J�\�[�h�̕��ω��x���v���b�g������炩�ȋȐ��łȂ����̂��} 2(��)�ł���
�\ 1:�J�\�[�h�d���ƃJ�\�[�h���x�̑Ή�
|
|
����ޓd�� |
�J�\�[�h���x(��C) |
|
|
|
|
(A) |
|
���ϒl |
|
|
|
2.6 2.8 3.0 3.2 3.4 3.6 3.8 4.0 4.2 4.4 |
1250 1184 1271 1260 1295 1330 1305 1380 1390�@1445 1435 1470 1480 1490 1520 1535 1627 1555 1585 1690 1592 1620 |
1217 1266 1313 1343 1418 1453 1485 1528 1589 1634 |
|
�܂���������@(1)�œ���ꂽ�f�[�^�͕\ 2�̂Ƃ���ł��顂�����O���t�ɂ����̂���} 3�ł��褗��ΐ��O���t�ɂ����̂���} 4�ł���
|
�\ 2:�e�J�\�[�h�d���ɂ�����z�ɓd���Ɨz�ɓd���̑Ή� |
|||||
|
|
|
|
|
|
|
|
�@ |
�J�\�[�h�d��I |
�@ |
�@ |
(A) |
|
|
�@ |
3.8
|
3.9
|
4.0
|
4.1
|
4.2
|
|
�z�ɓd��Vp(V) |
�z�ɓd��Jp |
�@ |
�@ |
(mA) |
|
|
0.0 |
0.10 |
0.05 |
0.09 |
0.08 |
0.10 |
|
1.0 |
0.20 |
0.12 |
0.15 |
0.17 |
0.15 |
|
2.0 |
0.25 |
0.25 |
0.27 |
0.29 |
0.30 |
|
3.0 |
0.40 |
0.40 |
0.40 |
0.41 |
0.48 |
|
4.0 |
0.55 |
0.58 |
0.60 |
0.60 |
0.61 |
|
5.0 |
0.70 |
0.72 |
0.75 |
0.80 |
0.80 |
|
6.0 |
0.90 |
0.91 |
1.00 |
1.00 |
1.01 |
|
7.0 |
1.05 |
1.12 |
1.20 |
1.25 |
1.28 |
|
8.0 |
1.25 |
1.35 |
1.48 |
1.50 |
1.53 |
|
9.0 |
1.45 |
1.62 |
1.70 |
1.80 |
1.79 |
|
10.0 |
1.70 |
1.89 |
2.00 |
2.05 |
2.09 |
|
11.0 |
1.88 |
2.12 |
2.35 |
2.38 |
2.42 |
|
12.0 |
2.10 |
2.42 |
2.63 |
2.70 |
2.71 |
|
13.0 |
2.30 |
2.69 |
2.90 |
3.05 |
3.09 |
|
14.0 |
2.43 |
2.99 |
3.28 |
3.40 |
3.45 |
|
15.0 |
2.60 |
3.30 |
3.70 |
3.75 |
3.85 |
|
16.0 |
2.70 |
3.61 |
4.00 |
4.15 |
4.20 |
|
17.0 |
2.72 |
3.88 |
4.40 |
4.58 |
4.65 |
|
18.0 |
2.79 |
4.25 |
4.80 |
4.95 |
5.10 |
|
19.0 |
2.80 |
4.50 |
5.28 |
5.40 |
5.55 |
|
20.0 |
2.82 |
4.88 |
5.80 |
5.81 |
6.10 |
|
25.0 |
2.90 |
5.93 |
8.0 |
8.32 |
8.65 |
|
30.0 |
2.98 |
6.21 |
9.8 |
10.8 |
11.4 |
|
35.0 |
3.00 |
6.38 |
11.6 |
13.3 |
14.1 |
|
40.0 |
3.02 |
6.48 |
14.0 |
16.0 |
17.2 |
|
45.0 |
3.05 |
6.54 |
15.2 |
18.6 |
20.2 |
|
50.0 |
3.08 |
6.60 |
15.4 |
21.2 |
23.2 |
|
55.0 |
3.10 |
6.65 |
15.8 |
23.8 |
26.5 |
|
60.0 |
3.10 |
6.70 |
16.0 |
26.2 |
29.9 |
|
65.0 |
3.11 |
6.74 |
15.8 |
27.6 |
33.5 |
|
70.0 |
3.14 |
6.80 |
16.2 |
28.5 |
37.0 |
|
75.0 |
3.13 |
6.82 |
16.0 |
29.0 |
40.5 |
|
80.0 |
3.13 |
6.88 |
16.4 |
29.2 |
44.0 |
|
85.0 |
3.15 |
6.90 |
16.4 |
29.5 |
47.5 |
|
90.0 |
3.18 |
6.92 |
16.4 |
29.9 |
50.5 |
|
95.0 |
3.19 |
6.97 |
16.6 |
30.0 |
52.9 |
|
100.0 |
3.20 |
6.99 |
16.6 |
30.0 |
54.2 |
|
105 |
�@ |
7.10 |
16.4 |
�@ |
55.7 |
|
110 |
3.22 |
7.10 |
16.4 |
30.3 |
56.2 |
|
115 |
�@ |
7.12 |
�@ |
�@ |
56.8 |
|
120 |
3.22 |
7.15 |
16.4 |
30.5 |
57.0 |
|
130 |
3.25 |
7.20 |
16.4 |
30.9 |
57.5 |
|
140 |
3.28 |
7.20 |
16.4 |
31.0 |
58.0 |
|
150 |
3.29 |
7.25 |
�@ |
31.1 |
58.5 |
|
160 |
3.30 |
7.25 |
16.4 |
31.2 |
58.9 |
|
170 |
3.30 |
7.25 |
�@ |
31.3 |
59.2 |
|
180 |
3.32 |
7.30 |
17.0 |
31.5 |
59.5 |
|
190 |
3.32 |
7.40 |
�@ |
31.8 |
59.9 |
|
200 |
3.35 |
7.40 |
17.0 |
32.0 |
60.0 |
6)��͋y�ь��_
�} 3���e�J�\�[�h�d��������J�\�[�h���x�ɂ����ċ�ԓd�א�����Ԃ���щ��x������Ԃł���z�ɓd���͈̔͂ͤ�\ 3�̂Ƃ���ł���
�\ 3:�e�J�\�[�h�d���ɂ�������Ԃ��ꂼ��̏�Ԃł���z�ɓd���͈̔�
|
|
����ޓd��(����ނ̉��x) |
��ԓd�א������ |
���x������� |
|
|
|
3.8A(1758K) 3.9A(1775K) 4.0A(1801K) 4.1A(1832K) 4.2A(1862K) |
�ȏ� �ȉ� (V) 0.0~ 14.0 0.0~ 20.0 0.0~ 40.0 0.0~ 85.0 0.0~110 |
�ȏ� (V) 15.0~ 25.0~ 45.0~ 90.0~ 115 ~ |
|
|
��ԓd�א�����Ԃɂ����Đ} 4�̊e�J�\�[�h�d���̃O���t�͒����ƂȂ��Ă��顂��̌X��(��logJ��/��logV��)���ŏ����@�ł��Ƃ߂�Ƥ�\ 4�̂悤�ɂȂ�
�\ 4:�e�J�\�[�h�d���ɂ�������logJ��/��logV��
|
|
����ޓd��(����ނ̉��x) |
��logJ��/��logV�� |
|
|
|
3.8A(1758K) 3.9A(1775K) 4.0A(1801K) 4.1A(1832K) 4.2A(1862K) |
1.0 1.3 1.3 1.3 1.4 |
|
�����̒l�ɂ�莮[ 2]���瓾���� logJ��=(3/2)logV��+const. �ɂ�闝�_�l
��logJ��/��logV��=1.5���m���߂�ꂽ�
���x������Ԃɂ����Ď��@���
log(j��/�s�Q)=log�`-0.434(��/k�s) (j��:�O�a�d�����x) �c�c[ 3]
����������
�����Ť�J�\�[�h�̒��a��0.20mm��L����2.0cm��褂��̕\�ʐς�1.3�~10�|�Tm�Q�ł��顊e�J�\�[�h�d��������J�\�[�h�̉��xT �ɂ����鉷�x������ԓ��̗z�ɓd���Ɨz�ɓd���̑Ή�����ŏ����@�ɂ���ē���ꂽ�O�a�d��J��,�y�іO�a�d�����xj��,j��/T�Q,1/T �����ߤ�\�ɂ����̂��\ 5�ł���j��/T�Q���c��,1/T �������ɕБΐ��O���t�ɂ����̂���} 5(��)�ł���
�\ 5:�J�\�[�h�̊e���x�ɂ�����O�a�d��J��,�O�a�d�����xj��,j��/T�Q,1/T
|
|
����ޓd�� (����ނ̉��x) |
�O�a�d��J�� |
j��(A/m�Q) |
j��/T�Q (Am�|�QK�|�Q) |
1/T (K�|�P) |
|
|
3.8A(1758K) 3.9A(1775K) 4.0A(1801K) 4.1A(1832K) 4.2A(1862K) |
2.77mA 6.24 15.4 28.3 52.4 |
2.1�~10�|�W 4.8�~10�|�W 1.2�~10�|�V 2.2�~10�|�V 4.0�~10�|�V |
6.9�~10�|�P�T 1.5�~10�|�P�S 3.7�~10�|�P�S 6.5�~10�|�P�S 1.2�~10�|�P�R |
5.688�~10�|�S 5.634�~10�|�S 5.552�~10�|�S 5.459�~10�|�S 5.371�~10�|�S |
�܂��} 5�ɂͤ�v���b�g�����_��[ 3]���ɏ]�������ɂ̂�Ƃ��Ĥ�����������Ă��顒�
���̎��͍ŏ����@�ɂ���ċ��߂�꤂��̎���y=a+bx�kx=1/T,y=log(j��/T�Q)�l�Ƃ���Ƥ
a=7.2�}2.1 , b=(-3.7�}0.4)�~10�S �c�c(*)
�ł���
[ 3]�����a=log�`,b=-0.434�~��/k(�A�����̒P�ʂ�J)�ł��顂���Ĥ�����l����`�y�������v�Z�����(�A������eV�P��)���̂悤�ɂȂ褂��ꂪ���_�ł���
�^���O�X�e���̎d������=7.4�}0.8(eV)
�萔�`=1.8�~10�V (Am�|�QK�|�Q)
�ka�̍Ŋm�l�ɂ��v�Z���ʁl
2.3�~10�X (Am�|�QK�|�Q)
[a�̌덷���ő���ɏ���ɍl�����v�Z����]
1.3�~10�T (Am�|�QK�|�Q)
[a�̌덷���ő���ɉ����ɍl�����v�Z����]
7)�����ƍl�@
�����ߒ��y�ё��葀��ɂ����ĕs�K�ł������_�͍l�����Ȃ��
�L�������͏��Ȃ��Ƃ��J�\�[�h�̕\�ʐς̗L��������2���ł��邱�ƂɋN�����2���ł���
���̐^�l��4.6eV�ł����`�̐^�l��1.2�~10 Am�|�QK�|�Q�U�ł��顂���Ď����œ���ꂽ�l�̑��Ό덷���l����ƕ\ 6�̂悤�ɂȂ�
�\ 6:���Ό덷 (�P��:��)
|
|
|
�Ŋm�l�� ������ |
�ő� �ŏ� |
|
|
|
�� �` |
63 1.3�~10�R |
80 47 1.9�~10�T 0 |
|
�\ 6���番����悤�ɤ�����̌��ʂ͎U�X������̂ł�������A����`�̑��Ό덷���傫�����Ƃɂ��Ăͤ���̕K�R������q����
�덷�̗v���ɂ��čl���顑S�ʂɂ��������̂Ƃ��Ăͤ�܂��J�\�[�h���x�̑���ɂ��顕l���Ƌ��������ҍ����͕\ 1�̒��ɏq�ׂ��Ƃ��褊e��1���肵��(�A����ŏ���2��̑���ɂ�蒘�������l�̊J�����ł�4.2A,4.4A�ɂ��Ă͉�����***�������1��)�4.2A,4.4A�ȊO�̃J�\�[�h�d���ł����Ȃ�̑���l�̊J������������������l�̉�͂Ɏ�Ɏg��ꂽ3.8A,4.0A,4.2A�ɂ����Ĥ3.8A,4.0A�ł͗�����l�̍��͏��Ȃ��4.2A�ɂ��Ă�3�肵�Ă��邽�ߌ덷�ւ̉e���͔����ł���
�܂����ԓd�א�����Ԥ���x������Ԃ̋敪�������顂���ͤ
�J�\�[�h�d��4.1A,4.2A�ɂ����ċ敪���̌���ɖ��������邱�Ƃł��顐} 3���番����悤�ɓ���4.1A�ɂ����Ă͂��Ɨz�ɓd����15V�Ⴂ�_���牷�x������Ԃł���Ƃ��l�����邩��ł��顂܂���O�a�d��J���̌���ɍŏ����@��p���Ă��邪��덷�͊�������Ŋm�l�̂L���Ă���
���y���`�̌v�Z�Ɋւ�����̂Ƃ��Ăͤ�} 5��5�_�����v���b�g�ł��Ȃ��������Ƃ����顕W�{�����Ȃ����瓖�R�덷���傫���Ȃ�
���Ĥ�`�̑��Ό덷���傫�����Ƃɂ��Ăł��邪�����͉�X�̎����̎d���⑪��l�̓ǂݎ������������Ƃ�������邪����̎�̌덷������d�g�݂�[ 1]����蓱�������ꂽ[ 3]���ɏ]��������l�̌v�Z�����ߒ��ɂ���Ƃ����K�R�I�Ȗʂ����顂܂���} 5�̉����̒l���W��������������̏W�����Ă���͈͂�x=0(K�|�P)���痣��Ă���(*)��a�͕Бΐ��O���t��̒�����y�ؕЂł��褑O�q�̗v���ɂ�蔭�������덷���������x=0�܂ň������������Ƃő��������
���̂�����`�̌v�Z���@�� �`=10�� �ł��題덷�͎w���v�Z���o�Ĥ�啝�ɖc��オ�顂���ɑ��Ό덷�̌v�Z�@�� �덷/�^�l �ł��邩�礔���ȑ��Ό덷�ƂȂ����
<�ȁ@��>
Copyright(C) 2000 TAKAGI-1 All rights reserved.