����[�U�[����p������������|�[�gWeb��
![]()
����[�U�[����p����������ͤ�ȉ��̈قȂ�2��ނ̎�������Ȃ�
���� 1:�P�X���b�g�ɂ����
���� 2:�Ό��t�B���^�ɂ�钼���Ό��̊m�F
�@���� 1:�P�X���b�g�ɂ���܁@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
1-1)�����ړI
�{�����ͤ�P�X���b�g�ɂ�郌�[�U�[����܂��s������̉�܌����x���z�̎����l�Ɨ��_�l�Ƃ̔�r���s�����Ƃ�ړI�Ƃ���
1-2)�����̌���
��܌��ۂ̈��Ƃ��Ĕg���Ƃقړ�����a�̒P�X���b�g�ɕ��ʔg����˂���P�X���b�g����̏\���ɗ��ꂽ�ʒu�ł̉�ܔg�̋��x���ϑ�����ꍇ�ɂ��Ĥ���ꂩ��q�ׂ顒A����X���b�g�͒��������ɂ͖����ɒ������̂Ƃ��顂܂���} 1- 1�ɒP�X���b�g�y�уX�N���[���̐����f�ʐ}�������
�} 1- 1:�P�X���b�g�y�уX�N���[���̐����f�ʐ}(��)
���̏ꍇ�AB�̂�����_�ɂ����ēd��̈ʑ��͈��ł��顐} 1- 1�̂悤�ɓ��ˌ��̐i�s���������̊p�x���Ȃ������ŃX�N���[����̓_P�ɒB�����ܔg��AB��̊e�������瑗��o�����g�������������̂ł��顐} 1- 1��x����x+dx�̔����̈悩�瑗��o���ꂽ�g��A���瑗��o���ꂽ�g�����H��x�sin�������̂�2��x�sin��/��(rad)�����ʑ����x���P�ɒB���顂���Ĥ�_P�ɒB�����ܔg�̓d���
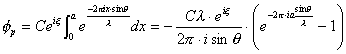
(��:�_Q�Ɠ_P�ł̈ʑ��� ��:���˔g�̔g�� �b:���˔g�̐U���ɔ�Ⴗ��萔)
�ƕ\�����
���������Ĥ�_P�Ŋϑ�������܌����x��
I�o=|���o|�Q=C�Qa�Q(sin�Q��)/���Q (�A������߃�a�sin��/��)�@�c�c[ 1]
�ƕ\�����
����Ĥ���xI�o����=m������
a�sin��=m�� (m��0�ȊO�̐���)�@�c�c[ 2]
�̂Ƃ���ɏ��l0���Ƃ邱�ƂƂȂ顒P�X���b�g�ƃX�N���[���Ƃ̋�����L����[�U���ƃX�N���[���̌����_����X�N���[����̓_P�܂ł̋�����y�Ƃ����
tan��=(y-a/2+x)/L�`y/L �ƂȂ�̂Ťy<<L�̏ꍇ�sin���`tan���`y/L�Ť���`��ay/��L�ł��褉�܌����xI�o�ͤ
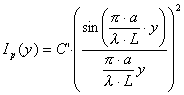 �@�c�c[ 3]
�@�c�c[ 3]
(�A���C�L:�s�[�N���x C�L=C�Qa�Q)
�Ƥ�\�����
����ɤ�ɏ��l�̏�����[ 2]��
y=m��L/a�@�c�c[ 4]
�Ƃ��\����ɑ�l�͇@��������cos��-sin��=0���������Ɍ���邱�Ƃ������顂���ĤC�L�ŋK�i��������܌����xI�o/C�L�̋ɑ�l���v�Z����܂Ƃ߂�Ƥ�\ 1- 1�̂Ƃ���ƂȂ�
�\ 1- 1:���_��蓱���o���ꂽ�K�i�����ꂽ��܌����x(I�o/C�L)�̋ɑ�l
|
|
��������
|
I�o/C�L (�~10�|�R) |
|
|
|
0 1 2 3 4 5 |
1000 47.2 16.7 8.33 5.01 3.35 |
|
1-3)�������u
�{�����ł͈ȉ��ɂ����鑕�u���g�p�����
�����[�U�[���U��
�{�� NEC GLG 5380 (He-Ne���[�U�[ �o��2mW �g��632.8nm)
���[�U�[�p��p�d�� NEC GLS 5370
�����[�U�[�����p���w�n
��^�A���~���w�x���` ��-01
��܃X���b�g(�P�X���b�g)
����X���b�g
�����d�f�q
Si�t�H�g�_�C�I�[�h S2386-8K
���f�W�^���}���`���[�^�[ HEWLETT PACKARD 34401A US36094223
�܂����L�̑��u��} 1- 2�ɂ悤�ɔz�u�����
�} 1- 2:���u�̔z�u�}(��)
1-4)�������@
�P�� ��
( 1)��܃X���b�g�Ƥ���o��(���d�f�q)�Ƃ̋�����1.00m�ƂȂ�悤�ɍ��킹���
( 2)��܃X���b�g��傫���J������X�e�[�W�����_�ɍ��킹����ԂŤ���[�U�[�������o��̉��������ɗ���悤���[�U�[�z���_�[�̂Ƃ߃l�W�߂����
( 3)��܃X���b�g��������������[�U�[�����X���b�g�ɋϓ��ɓ����褃X�N���[����ɍ��E�Ώ̂ȉ�܃p�^�[���������悤�ɤ���[�U�[�z���_�[������ɒ��߂����
�Q��܃v���t�@�C���̑���
( 1)���[�U�������傤�Ǐ�����Ƃ��̉�܃X���b�g��a�O���L�^�����
( 2)��܃X���b�g���̖ڐ����0.11mm�ɍ��킹���
( 3)�f�W�^���}���`���[�^(DMM)�̒[�q�ג�R�ɐڑ�������x���ő�ɂȂ�ʒu�ɉ��X�e�[�W���ړ���������̏�Ԃ�DMM�̕\���d���l��400mV�ȉ��ł��邱�Ƃ��m�F�����
( 4)���X�e�[�W��-50.0mm����+50.0mm�܂�1.0mm�Ԋu�ňړ�������e�ʒu�ł̕��ג�R�d���l��DMM�ő��肵��L�^�����
1-5)����f�[�^
���[�U�������傤�Ǐ�����Ƃ��̉�܃X���b�g��a�O��0.02mm�ł����������Ĥ�����I�ȃX���b�g����0.09mm�ł���
���肳�ꂽ�f�[�^�ͤ�\ 1- 2�̂Ƃ���ł��顂��̃f�[�^���c�����ʒu������ג�R�d���l�Ƃ��ăO���t�ɂ����̂���} 1- 3�ł��褂���2�������ȍ~�y��-2�������ȍ~(�X�e�[�W�ʒu�̒l���s�[�N���x���Ƃ�ʒu�̒l��菬�����̈�ɂ����閾���y�шÐ��̎������s�[�N���x���Ƃ�ʒu����߂�����-1���-2����c�c�ƌď̂�����̂Ƃ���)���g�債���̂��} 1- 4�ł���
|
�\ 1- 2:����f�[�^ |
|
�P��: |
�X�e�[�W�ʒu:mm |
||||
|
|
|
|
|
|
|
���ג�R�d���l:mV |
|
|
|
|
|
|
|
|
|
|
|
�X�e�[�W�ʒu |
���ג�R�d���l |
|
�X�e�[�W�ʒu |
���ג�R�d���l |
|
�X�e�[�W�ʒu |
���ג�R�d���l |
|
-50.0 |
1.187 |
|
-9.0 |
25.297 |
|
32.0 |
2.873 |
|
-49.0 |
0.952 |
|
-8.0 |
20.925 |
|
33.0 |
1.796 |
|
-48.0 |
0.765 |
|
-7.0 |
11.463 |
|
34.0 |
1.791 |
|
-47.0 |
0.734 |
|
-6.0 |
3.720 |
|
35.0 |
2.807 |
|
-46.0 |
0.881 |
|
-5.0 |
11.672 |
|
36.0 |
3.946 |
|
-45.0 |
1.208 |
|
-4.0 |
48.736 |
|
37.0 |
4.510 |
|
-44.0 |
1.538 |
|
-3.0 |
116.23 |
|
38.0 |
4.481 |
|
-43.0 |
1.782 |
|
-2.0 |
212.64 |
|
39.0 |
3.898 |
|
-42.0 |
1.789 |
|
-1.0 |
311.26 |
|
40.0 |
2.368 |
|
-41.0 |
1.535 |
|
0.0 |
374.36 |
|
41.0 |
1.784 |
|
-40.0 |
1.182 |
|
1.0 |
391.60 |
|
42.0 |
1.879 |
|
-39.0 |
0.935 |
|
2.0 |
397.74 |
|
43.0 |
2.508 |
|
-38.0 |
0.984 |
|
3.0 |
395.28 |
|
44.0 |
3.081 |
|
-37.0 |
1.357 |
|
4.0 |
382.01 |
|
45.0 |
3.416 |
|
-36.0 |
2.004 |
|
5.0 |
332.30 |
|
46.0 |
3.223 |
|
-35.0 |
2.541 |
|
6.0 |
224.59 |
|
47.0 |
2.666 |
|
-34.0 |
2.722 |
|
7.0 |
127.20 |
|
48.0 |
1.946 |
|
-33.0 |
2.448 |
|
8.0 |
55.189 |
|
49.0 |
1.633 |
|
-32.0 |
1.893 |
|
9.0 |
10.472 |
|
50.0 |
1.672 |
|
-31.0 |
1.326 |
|
10.0 |
0.731 |
|
|
|
|
-30.0 |
1.181 |
|
11.0 |
8.850 |
|
|
|
|
-29.0 |
1.626 |
|
12.0 |
21.332 |
|
|
|
|
-28.0 |
2.754 |
|
13.0 |
27.145 |
|
|
|
|
-27.0 |
4.000 |
|
14.0 |
25.888 |
|
|
|
|
-26.0 |
4.573 |
|
15.0 |
17.558 |
|
|
|
|
-25.0 |
4.325 |
|
16.0 |
8.414 |
|
|
|
|
-24.0 |
3.356 |
|
17.0 |
2.453 |
|
|
|
|
-23.0 |
2.172 |
|
18.0 |
1.335 |
|
|
|
|
-22.0 |
1.593 |
|
19.0 |
3.916 |
|
|
|
|
-21.0 |
2.334 |
|
20.0 |
8.070 |
|
|
|
|
-20.0 |
4.343 |
|
21.0 |
10.675 |
|
|
|
|
-19.0 |
6.965 |
|
22.0 |
10.330 |
|
|
|
|
-18.0 |
8.723 |
|
23.0 |
7.878 |
|
|
|
|
-17.0 |
8.783 |
|
24.0 |
4.007 |
|
|
|
|
-16.0 |
6.983 |
|
25.0 |
1.887 |
|
|
|
|
-15.0 |
3.855 |
|
26.0 |
1.642 |
|
|
|
|
-14.0 |
2.263 |
|
27.0 |
3.279 |
|
|
|
|
-13.0 |
3.502 |
|
28.0 |
5.298 |
|
|
|
|
-12.0 |
9.142 |
|
29.0 |
6.260 |
|
|
|
|
-11.0 |
16.767 |
|
30.0 |
5.985 |
|
|
|
|
-10.0 |
24.092 |
|
31.0 |
4.498 |
|
|
|
|
|
|
|
|
|
|
|
|
�O���t�}1-3,1-4
1-6)��͋y�ь��_
���ג�R�d���l��400mV�ȉ��Ȃ̂Ť���ג�R�d���l�ƌ��d�f�q�ɓ��˂��郌�[�U�[���̋��x�͔�Ⴕ�Ă���
���x�̋ɏ��l��^����ʒu��ǂݎ�褕\ 1- 3�ɂ܂Ƃ߂��
|
�\ 1-
3:�ɏ��l��^����X�e�[�W�ʒu�Ƃ��̈ʒu�ł̌����x |
|||||
|
|
|
���� |
�ʒu |
�����x
(mV) |
|
|
|
|
�@ |
(mm) |
(���ג�R�d��) |
|
|
|
|
-6 |
-47.0 |
0.734 |
|
|
|
|
-5 |
-39.0 |
0.935 |
|
|
|
|
-4 |
-30.0 |
1.18 |
|
|
|
|
-3 |
-22.0 |
1.59 |
|
|
|
|
-2 |
-14.0 |
2.26 |
|
|
|
|
-1 |
-6.0 |
3.72 |
|
|
|
|
1 |
10.0 |
0.731 |
|
|
|
|
2 |
18.0 |
1.34 |
|
|
|
|
3 |
26.0 |
1.64 |
|
|
|
|
4 |
34.0 |
1.79 |
|
|
|
|
5 |
41.0 |
1.78 |
|
|
|
|
6 |
49.0 |
1.63 |
|
|
|
|
|
|
|
|
����ɕ\ 1- 3�̎���m�ƈʒuy�����O���t�Ƀv���b�g�����̂���} 1- 5�ł���
�O���t�}1-5
�{�}�ɂ��y����m�ɑ��Ď��ɕ\�����悤�ɒ����I�ɕω����邱�Ƃ��m�F���ꂽ����̒����̌X����8.0�~10�|�R(m)�ł��褂��ꂪ��L/a (a:�X���b�g��)�ɓ��������Ƃ���a���v�Z����Ƥ
a=7.9�~10�|�U(m)�ƂȂ顁@�c�c(*)
���Ƀo�b�N�O���E���h���xI�����ߎ��I�Ɉʒuy�̈ꎟ���ŕ\������̂Ƃ��Ĥ�\ 1- 3�̃f�[�^���礍ŏ����@��p���ċ��߂�Ƥ
I��=p+qy �kp=1.60�}0.24,q=(5.18�}7.68)�~10�|�R�l
�ƂȂ顂Ȃ��I���͐} 1- 4�ɂ����Ĥ�j���Ŏ�����Ă���(��)�
�����ċ��x�̋ɑ�l��^����ʒu�Ƃ��̈ʒu�ł̃o�b�N�O���E���h���x�������������ɑ�l�̒l(��܌��݂̂̋��x)��\�ɂ����̂���\ 1- 4�ł���
|
�\ 1-
4:�ɑ�l��^����X�e�[�W�ʒu�Ƃ��̈ʒu�ł̉�܌��݂̂̋��x |
||||||
|
|
|
�@ |
�@ |
��܌��݂̂� |
|
|
|
|
|
���� |
�ʒu |
���x�@�@�@�@(mV) |
|
|
|
|
|
�@ |
(mm) |
(���ג�R�d��) |
|
|
|
|
|
-5 |
-42.0 |
0.41 |
|
|
|
|
|
-4 |
-34.0 |
1.30 |
|
|
|
|
|
-3 |
-26.0 |
3.11 |
|
|
|
|
|
-2 |
-17.0 |
7.27 |
|
|
|
|
|
-1 |
-9.0 |
23.7 |
|
|
|
|
|
0 |
2.0 |
396 |
|
|
|
|
|
1 |
13.0 |
25.5 |
|
|
|
|
|
2 |
21.0 |
8.97 |
|
|
|
|
|
3 |
29.0 |
4.51 |
|
|
|
|
|
4 |
37.0 |
2.72 |
|
|
|
|
|
5 |
45.0 |
1.58 |
|
|
|
|
|
|
|
|
|
|
�܂��0���̋ɑ�l�ŋK�i�����������x��0���̋ɑ�l��^����ʒu����ɂ������ΓI�Ȉʒu�����Ƃߤ�\�ɂ����̂���\ 1- 5�ł���
|
�\ 1-
5:����l���瓱���o�����K�i�����ꂽ��܌����x |
|||||
|
|
|
���� |
���Έʒu |
�����x |
|
|
|
|
�@ |
(mm) |
(�~10-3) |
|
|
|
|
-5 |
-44.0 |
1.0 |
|
|
|
|
-4 |
-36.0 |
3.28 |
|
|
|
|
-3 |
-28.0 |
7.85 |
|
|
|
|
-2 |
-19.0 |
18.4 |
|
|
|
|
-1 |
-11.0 |
59.9 |
|
|
|
|
0 |
0.0 |
1000 |
|
|
|
|
1 |
11.0 |
64.3 |
|
|
|
|
2 |
19.0 |
22.6 |
|
|
|
|
3 |
27.0 |
11.4 |
|
|
|
|
4 |
35.0 |
6.86 |
|
|
|
|
5 |
43.0 |
4.00 |
|
|
|
|
|
|
|
|
|
|
�@ |
�u�������_�l���傫�����v�̎w�E���� |
|||
(*)�ŋ��߂��X���b�g��a��X���b�g�ƃX�N���[���̊Ԃ̋���L=1.00(m)����[�U���̔g����=6.328�~10�|�V(m)�0���̃s�[�N���xC�L=0.392(V)������ăX�e�[�W�ʒuy�L(y�L=y-2.0 ����ͤ0���̃s�[�N�ʒu���X�e�[�W�̖ڐ��茴�_�Ɉ�v���Ȃ�����)��[ 3]���ɑ������(�A��y�L�͂��̂܂�y�ɑ��)�����ꂽ�e�X�e�[�W�ʒu�ł̗��_��̋��x�ɤ���ꂼ��̈ʒu�ł̃o�b�N�O�����h���x�����Z�����l(�ȍ~�����_�I�ɑ��肳���ׂ��l��Ə̂���Ȃ��{�l�͕��ג�R�d���l�̌`�ŋ��x��\��)�����ߤ�c���ɂƂ�y�������Ƃ��ċȐ���`�������̓I�ɂͤ�Ȑ��͈ȉ��̕��@�ŕ`�����
( 1)�X�e�[�W�ʒu-50.0mm����50.0mm�܂ł�Ώۂ�0.1mm���݂ŗ��_�I�ɑ��肳���ׂ��l���v�Z�����
( 2)�����̓_��E��_�Ŏ�������ׂĂ̓_�����炩�ȋȐ��Ō��
�l�ͤ���̕��@�ŏ����ꂽ�Ȑ���-50.0mm����50.0mm�܂ł̂��ׂẴX�e�[�W�ʒu�ɂ����闝�_�I�ɑ��肳���ׂ��l�������Ɗm�M����
���̋Ȑ��y�ъe�v�Z�l��\���_��} 1- 3�ɏ������̂��} 1- 6�ł��褐} 1- 4�ɏ������̂��} 1- 7�ł���
�O���t�}1-6,1-7
1-7)�����ƍl�@
����l�Ɨ��_���瓱���o�����l�Ƃ��r����
< 1>���ۂ̎����I�ȃX���b�g���Ƥ(*)�ŋ��߂�a�Ƃ̔�r
���ۂ̎����I�ȃX���b�g��9.0�~10�|�Um��^�l�Ƃ���Ƥ(*)��a�̑��Ό덷��12���ł��顂���Ė{���ʂ͈������悭���Ȃ��̑Ó��������ƕl�͕]������
< 2>����l���狁�߂�ꂽ��܌��݂̂̋ɑ�l�̑����x�Ɨ��_��苁�߂��邻��Ƃ̔�r
�O�҂͕\ 1- 5�ɤ��҂͕\ 1- 1�Ɏ����Ă��顊e�����ɂ��ė��_�l��^�l�Ƃ������l�̌v�Z�������ʂ̑��Ό덷���v�Z����ƕ\ 1- 6�̂Ƃ���ɂȂ顂Ȃ�����Ό덷�̗�̂�����O��̓v���X�����̑����x�̑��Ό덷����̓}�C�i�X�����̂���ł��顂܂���{�\�Ɋւ��錟���ͤ��r< 3>���ɋL���
�\ 1- 6:�����x�̑��Ό덷
|
|
���� |
���Ό덷(��) |
|
|
|
1 2 3 4 5 |
36.3 27.0 35.5 9.91 36.7 5.82 37.0 34.6 19.3 69 |
|
< 3>�e�X�e�[�W�ʒu�ɂ������܌����x�̎����l�Ɨ��_�I�ɑ��肳���ׂ��l�Ƃ̔�r�y�ь���
�} 1- 6�Ɛ} 1- 7����Ɍ�҂�p���Ĕ�r��������s����Ȃ���덷�̗v���ɂ��Ă͖{�區�ڂ̉�����(����)�̕����ɂ������Ă���
�Ⴂ���ڗ��̂͋ɑ�l�ɂ����鋭�x�ł���(�u���̌덷�ɂ��Ă͓��ˌ����[�U�[�̋��x�������������ߓd���l�ƌ����x�Ԃ̔��W������Ă��邱�ƂɋN������Ǝv���܂��v�Ƃ̃R�����g����)�B���̌����͉�܌��݂̂̑����x�̌덷�ƃo�b�N�O���E���h���x�̌덷�ł���
��܌��݂̂̑����x�̌덷�ͤ�\ 1- 6�̂Ƃ���Ť����31���ł��顕l�ͤ���̒l���o�����߂̌v�Z�ߒ������������l�����Ăऐ[���Ȍ덷�ł��鎖�ɂ͑���Ȃ��ƍl������ʂ̑Ó��������Ⴍ�]������
���̌덷�̗v���Ƃ��Ăͤ�ɑ�l�̒l(�\ 1- 4)�ɂͤ�\������������ƃX�e�[�W�ʒu1.0mm�P�ʂő��肵�����ג�R�d���l�݂̂����g���Ȃ����Ƥ�e�ɑ�l�̑���ɂ�����덷(���Ƀs�[�N���x�̑���̌덷�͂��ׂĂɂ�������Ă���)����l�����顎����̏������ɂ��̂͑O�҂̤�����̑傫�Ȃ��̂͌�҂̉e����傫���顂��������L��2�v��������30�����̌덷�ނƂ͍l���ɂ����������ł��邱�Ƃ͊m���ł���ƍl����
�����Ńo�b�N�O���E���h���x�̌덷�ɂ��Ăͤ�e�ɏ��l���݂���̌덷�����̂܂܌���Ă��顋ɑ�l�Ɠ��l��o�b�N�O���E���h���x�̊������߂邽�߂̋ɏ��l�̒l(�\ 1- 3)�ɂͤ�\������������Ƥ�X�e�[�W�ʒu1.0mm�P�ʂő��肵�����ג�R�d���l�݂̂����g���Ȃ���X�e�[�W�ʒu�̔����ȕω��ő傫�����x�̂����1���-1���̋ɏ��l�͐M�����̒Ⴂ���̂ƂȂ褕l�͂��ꂪ�덷�ݏo���Ă���ƍl���顂܂���o�b�N�O���E���h���x�̈ꎟ���͂����܂ł��ߎ��ɉ߂��Ȃ����Ƃ��덷�ݏo������ł���
�����ɑ�l��ɏ��l���Ƃ�X�e�[�W�ʒu�̈Ⴂ��1.0mm�ȉ��ƂȂ褑���l�͗��_�l�ɏ]�������̂ƂȂ����
�����ߒ��y�ё��葀��ɂ����ĕs�K�ł������_�̓f�W�^���}���`���[�^�[�̓d���w���l���������Ȃ��܂܂�݂Ƃ������Ƃł��顂�������l�̓��ǂ̕ʂ̃e�[�u���̎����҂͎��� 2�ɂ����Ďw���l����������̂�҂��Ă���������̑���ɖ�2��������Ƃ̂��Ƃ����������ĕl�͂���͎d���̂Ȃ����Ƃł���ƍl�����i�uDMM�̎w���l�̗h�炬�̓��[�U�[�����x�̗h�炬�ɉ����Ă���̂Ŏ�������悤�Ȃ��̂ł͂Ȃ��Ǝv���܂��v�Ƃ̃R�����g����j�B
�L�������͏�L�̂��Ƃ��l�����ג�R�d���l�̑���l���g���v�Z�ł͓�����l�̗L��������3���ɐݒ肵����ȍ~�̌v�Z�͊e���Z�ɂ�����L�������̎�舵���ɂ�����������A����o�b�N�O���E���h���x�̈ꎟ�������߂�ۂͤ�{���O���t����ǂݎ��ׂ��l�Ȃ̂Ť�L������3���Ƃ����
���ʂ̑Ó����̕]���ͤ���ɖ{�區�ڒ���< 1>�< 3>�ɏq�ׂĂ���
�덷�̗v��(����)�ͤ�{���ڂ�< 3>���ɏq�ׂ����Ƃ��܂��L�顂܂�������< 3>���ɒ[�I�ɐG�ꂽ����L�����������������Ă���͂�f�W�^���}���`���[�^�[�̓d���w���l���������Ȃ��܂ܓǂ݂Ƃ������Ƃɂ��덷���ˑR�Ƃ��đ��݂��Ă���ƕl�͍l���顂���ɤ���[�U�[������C����i�ލۂɋ�C���̂ق���ŎU�����Ă��邱�Ƃ�����ƍl���顎��ۤ���������[�U�[�����ʂ��Ă����ԂɐԂ������������Ȃق��肪�ώ@���ꂽ�
<����
1�ɂ��ďI���>
�@���� 2:�Ό��t�B���^�ɂ�钼���Ό��̊m�F
2-1)�����ړI
�{�����̓��[�U�[���̒����Ό���Ό��t�B���^�ɂ���Ċm�F���邱�Ƃ�ړI�Ƃ���
2-2)�����̌���
���[�U�[���ͤ���̓d��x�N�g���̕��������Ť�����Ό����Ă��顂��̂��Ƃ��m���߂邽�ߤ�Ό��t�B���^�̒ʉߌ��̋��x�𑪒肷��
���[�U�[���̓d��x�N�g��E��A�����Ƃ���Ό��t�B���^��ʉ߂ł�����̓d��x�N�g���̕�����B�����Ƃ���A������B�����͌�_�ɂ����Ċp�x�����Ȃ�����̂Ƃ����[�U�[����B����������E�cos���Ť���̋��x�͓d��x�N�g���̑傫����2��ɔ�Ⴗ�邩�礕Ό��t�B���^�̒ʉߌ��̋��x��cos�Q���ɔ�Ⴗ��
2-3)�������u
�{�����ł͈ȉ��ɂ����鑕�u���g�p�����
�����[�U�[���U��
�{�� NEC GLG 5380 (He-Ne���[�U�[ �o��2mW �g��632.8nm)
���[�U�[�p��p�d�� NEC GLS 5370
�����[�U�[�����p���w�n
��^�A���~���w�x���` ��-01
�Ό��t�B���^
����X���b�g
�����d�f�q
Si�t�H�g�_�C�I�[�h S2386-8K
���f�W�^���}���`���[�^�[ HEWLETT PACKARD 34401A US36094223
�܂����L�̑��u��} 2- 1�̂悤�ɔz�u�����
�} 2- 1:���u�z�u�}�i���j
2-4)�������@
( 1)�Ό��t�B���^������[�U�[�����x�ɑΉ������d���l���ŏ��̓_�����������Ĥ���̂Ƃ��̕Ό��t�B���^�̊p�x���O��ǂ݂Ƃ�����܂�����̂Ƃ��̓d���l��ǂݎ��V�O�Ƃ����
( 2)�p�x�����O����5�x�����₵�Ă�������ꂼ��̊p�x�ɂ�����d���lV ���L�^�����
2-5)����f�[�^
���肳�ꂽ�f�[�^�͕\ 2- 1�̂Ƃ���ł���
|
�\ 2- 1:����f�[�^ |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
���@=161.9(��) V
=0.531(mV) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
��(��) |
V(mV) |
|
|
|
|
|
|
166.9 |
1.265 |
|
|
|
|
|
|
171.9 |
3.495 |
|
|
|
|
|
|
176.9 |
7.521 |
|
|
|
|
|
|
181.9 |
12.513 |
|
|
|
|
|
|
186.9 |
19.735 |
|
|
|
|
|
|
191.9 |
28.035 |
|
|
|
|
|
|
196.9 |
37.028 |
|
|
|
|
|
|
201.9 |
44.653 |
|
|
|
|
|
|
206.9 |
52.813 |
|
|
|
|
|
|
211.9 |
62.236 |
|
|
|
|
|
|
216.9 |
72.558 |
|
|
|
|
|
|
221.9 |
80.325 |
|
|
|
|
|
|
226.9 |
88.932 |
|
|
|
|
|
|
231.9 |
95.953 |
|
|
|
|
|
|
236.9 |
103.236 |
|
|
|
|
|
|
241.9 |
104.863 |
|
|
|
|
|
|
246.9 |
107.202 |
|
|
|
|
|
|
251.9 |
110.757 |
|
|
|
|
|
|
256.9 |
113.127 |
|
|
|
|
|
|
261.9 |
111.207 |
|
|
|
|
|
|
266.9 |
105.627 |
|
|
|
|
|
|
271.9 |
100.217 |
|
|
|
|
|
|
276.9 |
91.752 |
|
|
|
|
|
|
281.9 |
82.736 |
|
|
|
|
|
|
286.9 |
71.682 |
|
|
|
|
|
|
291.9 |
61.236 |
|
|
|
|
|
|
296.9 |
54.525 |
|
|
|
|
|
|
301.9 |
46.384 |
|
|
|
|
|
|
306.9 |
38.331 |
|
|
|
|
|
|
311.9 |
29.521 |
|
|
|
|
|
|
316.9 |
21.632 |
|
|
|
|
|
|
321.9 |
14.237 |
|
|
|
|
|
|
326.9 |
8.388 |
|
|
|
|
|
|
331.9 |
4.157 |
|
|
|
|
|
|
336.9 |
1.495 |
|
|
|
|
|
|
341.9 |
0.580 |
|
|
|
|
|
|
|
|
|
|
2-6)��͋y�ь��_
sin(��-���O)=cos���ł��邩��V-V�O��sin�Q(��-���O)�����҂���顉�����sin�Q(��-���O)�c����V-V�O���Ƃ��Ĥ����l���O���t�ɂ���Ƥ�} 2- 2�ɂȂ�
�O���t�}2-2
���}���V-V�O��sin�Q(��-���O)���m�F���꤃��[�U�[���������Ό����Ă��邱�Ƃ���m�F���ꂽ�
2-7)�����ƍl�@
�} 2- 2�ɂ����Ĥ����l�̌v�Z���ʂ�����������ɊO���_�͌�������Ȃ���������Ƃ��Ăउ��̌덷�̗v���̉e���͈̔͂ł���ƕl�͍l���顂���Ĥ�} 2- 2�̑���l�̌v�Z���ʂ̎U�z�͒����ɋ߂��̂Ť���ʂ̑Ó����͍����ƍl����
�����ߒ��y�ё��葀��ɂ����ĕs�K�ł������_�ƗL�������ͤ���� 1�Ɠ����ł���
�܂���덷�̗v���ͤ���� 1�ɏ�����f�W�^���}���`���[�^�[�̓d���w���l���������Ȃ��܂ܓǂ݂Ƃ������ƂƤ���[�U�[������C����i�ލۂɋ�C���̂ق���ŎU�����Ă��邱�Ƃ�����ƍl������(�uDMM�̎w���l�̗h�炬�̓��[�U�[�����x�̗h�炬�ɉ����Ă���̂Ŏ�������悤�Ȃ��̂ł͂Ȃ��Ǝv���܂��v�Ƃ̃R�����g����)
<�ȁ@��>
Copyright(c) 2000 TAKAGI-1 All rights reserved