「Bordaの振子によるgの測定」レポートWeb版
![]()
1)実験目的
Borda振子を微小振動させ、その振動の周期を測定することによって、重力加速度の大きさgを求めることが本実験の目的である。
2)実験の原理
針金の長さを l 、金属球の半径を a とし、ボルダ振子全体を剛体として近似する。
一般に、剛体の質量を M 、剛体の重心と回転軸との距離を h
とし、この軸の周りの慣性モーメントを I とすると、回転軸と重心とを結ぶ直線が鉛直線となす角を θ として、 θ の角
振幅 α が十分小さいとき、周期 T は近似的に
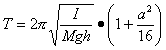
となる。
ボルダ振子の場合、針金の質量を無視すると、剛体の重心と金属球の重心が一致し、
I
= Mh2+2Ma2/5 , h = l
+ a が成立する。したがって周期Tは
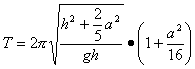
となり、周期 T から重力加速度の大きさ g を求めるには、本式を変形して
g
= 4(π/T)2 [h+2a2/(5h)] (1+a2/8) を使うこととなる。
短時間の実験では、振子の減衰を考えなくてよく、また測定開始時の角振幅をα1、測定終了時の角振幅をα2として、α2=α1α2と見なせるから、
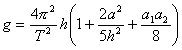 …[ 1]
…[ 1]
と、書ける。
3)実験装置・用具
( 1)支台 A……壁に取り付けてある
図 1:装置配置図 (略)
( 2)支座 B
( 3)刃先 C
( 4)針金と金属球
( 5)目盛板
( 6)望遠鏡
( 7)ノギス
( 8)長尺ノギス
( 9)時計……松下
TF83(7) B
(10)水準器……BORDA'S
PENDULUM TYPE BP-40
4)実験方法
( 1)支台Aのうえに支座Bをのせ、Bの3つのネジを調整して、Bを水平にした。その際水準器で水平の確認をした。
( 2)おもりをつけた針金の先端を刃先Cにつけて、おもりをつるし、CをBにまたがらせた。
( 3)おもりを静かにふらし10回の周期を測定した。
( 4)針金を刃先Cから外し、Cだけをふらし10回の周期を測定した。
( 5)( 3)と( 4)の周期が同じになるように刃先Cのネジを調節した。
( 6)再び針金の上端を刃先Cにつけ、Cを支座Bにまたがらせ、おもりを静かにつるした。
( 7)目盛板をおもりの背後に置き、約2m離れた机上に据えられた望遠鏡を、正面に針金と目盛板が見えるよう調整し、望遠鏡の焦点を針金に合わせた。
( 8)振子が静止しているときの針金の位置を目盛板でよみ、
b0 とした。。
( 9)振子を刃先と垂直な面内で振動させた。
(10)測定を行った。測定内容は以下のとおり。[()内、測定用具]
・周期測定の初めの振幅
b1 (目盛尺)
・振動回数が
0,10,20,……,190 回のときの時刻 (時計)
・周期測定の終わりの振幅
b2 (目盛尺)
・刃先から目盛尺までの距離
d (長尺ノギス)
・刃先からおもりの球面下端までの長さ
l + 2a (長尺ノギス)
・おもりの直径 2a 〔3回測定〕 (ノギス)
(11)違う実験者で手順(
9)、(10)を繰り返した。
5)測定データ
測定データは表 1から 5に示すとおりである。表 1、表 2が一回目の測定、表
3、表 4が二回目の測定により得られたデータである。また、 b0=0.00
cm であった。
|
1回目 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
表
1:測定データ1-1 |
|
|
|
|
|
表2:測定データ1-2 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
時刻 |
|
|
時刻 |
|
100周期の時間 |
|
|
測定内容 |
(cm) |
|
振動回数 |
分 |
秒 |
振動回数 |
分 |
秒 |
分 |
秒 |
|
||
|
0 |
15 |
57.6 |
100 |
19 |
9.9 |
3 |
12.3 |
|
d |
89.55 |
|
10 |
16 |
17.0 |
110 |
19 |
29.0 |
3 |
12.0 |
|
l+2a |
93.746 |
|
20 |
16 |
36.2 |
120 |
19 |
48.2 |
3 |
12.0 |
|
b1 |
2.80 |
|
30 |
16 |
55.8 |
130 |
20 |
7.8 |
3 |
12.0 |
|
b2 |
2.52 |
|
40 |
17 |
14.7 |
140 |
20 |
26.9 |
3 |
12.2 |
|
|
|
|
50 |
17 |
34.0 |
150 |
20 |
46.2 |
3 |
12.2 |
|
2a(1回目) |
3.98 |
|
60 |
17 |
53.6 |
160 |
21 |
5.6 |
3 |
12.0 |
|
2a(2回目) |
3.98 |
|
70 |
18 |
12.4 |
170 |
21 |
24.6 |
3 |
12.2 |
|
2a(3回目) |
3.98 |
|
80 |
18 |
31.6 |
180 |
21 |
43.6 |
3 |
12.0 |
|
a(平均値) |
1.99 |
|
90 |
18 |
51.0 |
190 |
22 |
3.2 |
3 |
12.2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2回目 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
表
3:測定データ2-1 |
|
|
|
|
|
表4:測定データ2-2 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
時刻 |
|
|
時刻 |
|
100周期の時間 |
|
|
測定内容 |
(cm) |
|
振動回数 |
分 |
秒 |
振動回数 |
分 |
秒 |
分 |
秒 |
|
||
|
0 |
30 |
13.5 |
100 |
33 |
25.2 |
3 |
11.7 |
|
d |
89.55 |
|
10 |
30 |
32.0 |
110 |
33 |
44.2 |
3 |
12.2 |
|
l+2a |
93.726 |
|
20 |
30 |
51.2 |
120 |
34 |
3.4 |
3 |
12.2 |
|
b1 |
2.60 |
|
30 |
31 |
10.6 |
130 |
34 |
22.8 |
3 |
12.2 |
|
b2 |
2.30 |
|
40 |
31 |
29.8 |
140 |
34 |
42.0 |
3 |
12.2 |
|
|
|
|
50 |
31 |
48.8 |
150 |
35 |
1.2 |
3 |
12.4 |
|
2a(1回目) |
3.97 |
|
60 |
32 |
8.2 |
160 |
35 |
20.6 |
3 |
12.4 |
|
2a(2回目) |
3.98 |
|
70 |
32 |
27.2 |
170 |
35 |
39.6 |
3 |
12.4 |
|
2a(3回目) |
3.99 |
|
80 |
32 |
46.6 |
180 |
35 |
58.6 |
3 |
12.0 |
|
a(平均値) |
1.99 |
|
90 |
33 |
5.6 |
190 |
36 |
18.0 |
3 |
12.4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
表
5:計算結果 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
_ |
|
|
|
|
|
|
|
|
|
|
|
T |
ΔT |
ΔT/T |
g |
2a2/(5h2) |
α1α2/8 |
|
||
|
|
|
(s) |
(×10-3) |
|
|
(m/s2) |
|
|
|
|
|
1 |
回目 |
1.921 |
3.79 |
1.97 |
×10-3 |
9.818 |
1.88 |
×10-4 |
1.10 |
×10-4 |
|
2 |
回目 |
1.922 |
7.06 |
3.67 |
×10-3 |
9.806 |
1.88 |
×10-4 |
0.932 |
×10-4 |
|
|
|
|
|
|
|
|
|
|
|
|
6)解析及び結論
表 1から 5のデータを計算処理した結果が、表 5である。 ![]() は周期の平均値、 ΔT
は周期の平均値の標準偏差である。
は周期の平均値、 ΔT
は周期の平均値の標準偏差である。
gの計算は[ 1]式による。なお、角振幅 α1=(b1-b0)/d , α2=(b2-b0)/d である。gはもちろんのこと、gの計算に用いた 2a2/(5h2) , α1α2/8 も表 5に記す。
7)検討と考察
hの値は 一回目…… 91.76 cm
, 二回目…… 91.74 cm であった。よって、有効数字から推定される誤差 Δh は、両回ともに
0.01 cm である。 また、両回ともに
Δh/h = 1.090×10−4 である。
ΔT と Δh より g にどれだけの誤差が発生するかを求めた。結果は、表
6のとおりである。
表 6: ΔT 及び Δh が g にもたらす誤差
(単位:m/s2)
-------------------------------------------------
g ΔTのもたらす誤差 Δhのもたらす誤差
-------------------------------------------------
1回目 9.818 ±0.039 ±0.001
2回目 9.806 ±0.072 ±0.001
-------------------------------------------------
表 6のそれぞれの誤差を相対誤差という観点でみると、表
7のとおりになる。
表 7:ΔT 及び Δh が g にもたらす相対誤差
(単位:%)
----------------------------------------
ΔTのもたらす相対誤差 Δhのもたらす相対誤差
----------------------------------------
1回目
0.39
0.010
2回目
0.74
0.011
----------------------------------------
ここで、表 5から 1+2a2/(5h2)+α1α2/8≒1 より、次式が成り立つ。
|Δg/g|〜2|ΔT/T|+|Δh/h|
よって、 |Δg/g|=
0.41 % (一回目) , 0.75 % (二回目) となる。本実験では各回において h を一回しか測らなかったこともあって、 g
へ ΔT からの影響が大きい。より精度を高めるには T の測定をより精密にせねばならない。本実験では二回目の
振動回数0回から100回での100周期の時間が平均値と差が大きく(系統誤差と考えてデータを放棄せよ、とのコメントあり)、ΔT を増す主な原因となっていると考える。
g の有効数字は、 b1 、 b2 、 a の有効数字は3桁だが、表 5の 2a2/(5h2) 、 α1α2/8 から計算される 1+2a2/(5h2)+α1α2/8 の有効数字が6桁であるため、 T 、 h の有効数字4桁に拘束され、4桁である。
実験過程及び測定操作において不適切であった点は、周期測定開始、終了時の振幅を測定するのに望遠鏡を使わず、直接、目盛板を見て測定したことがある。このことによる直接の誤差(
b1 、 b2 の誤差)は極めて微小であると考える。しかし、間接的に誤差を生んでいる可能性がある。このことについては下の「誤差の要因」
1) に述べる。
他には教科書の指示にしたがったかという点ではない。しかし、解析のためには
h の値を複数回求め、 Δh についてより精密に考えることができるように、 l+2a の値を a
と同様、3回測定するべきであった。
実験で求められたgと真値を比較する。gの真値は京都(北緯
35度 2分)において、
9.7971 m/s2 より、実験値の相対誤差は、表 8のとおりとなる。
表 8:真値と実験値との比較(相対誤差) (%)
|
|
最確値において |
相対誤差最大 |
相対誤差最小 |
|
一回目 |
0.21 |
4.26 |
0 |
|
二回目 |
0.08 |
7.68 |
0 |
表 8より二回目のほうが優秀な値を示したことがわかる。これは、実験の要領が分かってきたことによると考える。ただし、振子の等時性から逆算すると二回目の振動回数0回での時刻の計測には失敗したと考える。
全体としては、本実験の結果は真値との誤差が少なく、「成功した」と考える。
誤差の要因を下にあげる。
1)動くものを測定したこと
具体的には、各振動回数における時刻の測定、及び測定開始、終了時の振幅の測定である。瞬間的に読み取らねばならず、読み直しもできない。
また、「実験過程及び測定操作において不適切であった点」の「周期測定開始、終了時の振幅を測定するのに望遠鏡を使わず、直接、目盛板を見て測定したこと」が間接的に影響してくる。問題となるのは周期測定開始時である。本実験で周期測定開始時の各実験者の役割分担は
実験者 甲:おもりの指示、おもりの解放、 b1 測定、振動回数0の時刻測定
実験者 乙:振動回数0のカウント
であった。甲の作業が多いことが分かる。甲はこれらの作業を忙しくこなさねばならず、誤差がうまれやすくなっている。
2)式[ 1]を導くうえでおいた前提
具体的には、ボルダ振子全体を剛体として近似したこと、針金の質量を無視したことである。
<以上>
Copyright(C)
2000 TAKAGI-1 All Rights
Reserved.