2004年 8月 (ただし、その後 一部修正)

戻る

気象庁メソ数値予報の発展について

1.　緒言

　気象庁は、2004年7月22日、現業のメソ数値予報モデル(Meso Spectral Model あるいは Meso-Scale Model : MSM 。以下、単に「メソモデル」と記す)に替えて、2004年9月より新しいメソモデルの運用を開始すると発表した⁽¹⁾。

メソモデルは気象庁の現業数値予報モデルのひとつであり、全球スペクトルモデル（GSM）の娘モデルである領域スペクトルモデル（RSM）のさらに娘モデルである。予報領域は日本周辺で、水平解像度は10kmであり、防災気象情報の作成に使用されている。現業運用が開始されたのは、2001年3月である⁽²⁾。なお、気象庁は中期的重要課題のひとつとして「局地的豪雨等のメソ気象現象の的確な予報」を挙げている⁽³⁾。

メソ数値予報について調べると、近年、数値予報モデル以外にも大きな改良が行われていることが分かった。本レポートでは、新しいメソモデルと、メソ数値予報に近年実施された主な改良について述べる。

2.　新しいメソモデルについて

2.1.　概要

　新しいメソモデルは、気象研究所／数値予報課統一非静力学モデル(MRI/NPD-NHM)の並列版をベースとして、現業に使用する目的で開発が行われてきた非静力学メソモデル⁽⁴⁾である。

その特徴は、

l 静力学近似が用いられていない点

l 精密に雲物理が取り扱われている点

である⁽¹⁾。§2.2、2.3にこれら2つの特徴について記すが、気象庁から新しいメソモデルについて一般に発表された資料は、私の知る限りにおいて、文献(1)のみである。そこで、
§2.2、2.3を、ベースとなったMRI/NPD-NHMに関する資料を主に参考にし、それらの点についてMRI/NPD-NHMと新しいメソモデルが共通していると考えて記したことを予め断っておく。

　なお、「静力学近似が用いられていない」特徴から、新しいメソモデルは、非静力学数値予報モデル(NonHydrostatic Model : NHM)と呼ばれている。本レポートでは、以降、新しいメソモデルを「NHM」と記し、現業メソモデルを「MSM」と記す。MSMとNHMの主な仕様の違いを表1に示す。

表1: MSMとNHMの主な仕様の違い⁽⁵⁾

2.2.　特徴「静力学近似が用いられていない点」に関して

　NHMの基礎方程式は、

l 水平方向の運動量方程式:
　,

l 鉛直方向の運動量方程式:
　　　　　　　　　　　　　　…(1)

l 連続の式:

l 熱力学方程式:

l 状態方程式:

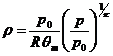
である。但し、dif. は拡散項を表し、添え字aは湿潤空気(乾燥空気と水蒸気の混合)、rは雨、sは雪、gは霰(あられ)、cは雲水、iは雲氷、vは水蒸気を表す。gは重力加速度、Vは終端速度(mass-weighted bulk terminal velocity)、qは混合比〔正確にはq＝(単位体積湿潤空気に含まれる質量)／(湿潤空気密度)〜(混合比) 〕、θは温位、Qは非断熱加熱率、Rは乾燥空気の気体定数、p₀は標準気圧、κは比熱容量比（C_p／C_v）である。θ_mは質量仮温位(mass-virtual potential temperature)と呼ばれ、
θ_m＝θ (1＋0.61q_v) (1−q_c−q_r−q_i−q_s−q_g) である。NHMでは、これらの方程式に地図投影、すなわち地球の丸みを考慮して支配方程式としている⁽⁶⁾。

一方、すべての気象庁現業モデルには、鉛直方向に静力学近似が用いられている⁽⁷⁾。言い換えれば、NHMは、気象庁で初めての現業非静力学モデルである。鉛直方向に静力学近似が用いられている方程式系をプリミティブ(primitive)方程式といい、プリミティブ方程式を使った数値予報モデルをプリミティブモデルという⁽⁷⁾。

静力学近似(静力学平衡近似)とは、気圧傾度力と重力がつりあっていると仮定する近似である。この近似により、鉛直方向の運動量方程式は、式(1)の代わりに
　　　　　

となる⁽⁸⁾。

静力学近似は、現象の水平スケールがその鉛直スケールよりも十分に大きい場合、現象とよく一致する。このため、一般の気象現象（水平スケール100km以上）において、この近似は適切である。

しかし、メソ数値予報の水平スケール解像度は10kmであり、メソモデルによって表現される現象の水平スケールは数十kmである（一般に解像度の5〜10倍程度の長さが、そのモデルによって表現可能な現象の最小スケールだといわれる）。一方、鉛直スケールに関しては、例えば、発達した積乱雲の鉛直スケールは10km以上になる⁽⁹⁾。積乱雲はメソモデルによって表現されるが、その水平スケールが鉛直スケールよりも十分に大きいというわけではないので、静力学近似により誤差が生じる。よって、静力学近似を用いないNHMの導入によりメソ数値予報の精度が向上する。

さらに、気象庁では、2006年3月にスパコンの更新を予定している。それに伴いメソ数値予報の水平スケール解像度は5kmとなるため、モデルで表現され且つ静力学近似により誤差が生じる現象の絶対数が多くなる。NHMの導入は、スパコン更新をもにらんだ実施である^{(1), (7)} 。

2.3　特徴「精密に雲物理が取り扱われている点」に関して

　MSMでは、凝結した水蒸気はすべて降水になり、直ちに地上に達するとみなされる。一方、NHMでは、雲物理がMSMよりも精密に考慮される。ただし、雲粒の径はExplicitには考慮されない。つまり、Bulk法が用いられる。

　NHMでは、降雨に関して、計算格子内に存在する雨水のバルク量を降下させるBox-Lagrangian rain drop schemeが用いられる。即ち、

　　　　　

である。離散時刻m (上付き添字で使われる)における鉛直方向k番目の計算格子(上側境界高度Z_k)において、
　　　　　
である⁽¹⁰⁾。

　NHMでは、気温減率がΓ_cを超え、かつ相対湿度RHが定数RH_iを超えた場合、気温減率がΓ_cに調節され、RHと全熱エネルギーが保存される。これは湿潤対流調節スキームと呼ばれる。なお、対流調節とは、積雲対流による水蒸気の潜熱の解放や熱の鉛直輸送などの効果を簡単に大規模運動に取り入れる方法である⁽¹¹⁾。Γ_cは、乾燥断熱減率Γ_dと湿潤断熱減率Γ_Sを用いて、
　　　　　　　for RH ＞RH_i
と表される。湿潤対流調節スキームとPrognostic explicit schemeを合わせることで、過飽和度ΔSはGrid scaleにおいて急減することなく、雲水の混合比q_cは、
　　　　　　　for k1≦k≦k2
と調節され、ΔSは、
　　　　　　　for k1≦k≦k2
となる。ここで、Δq_kは鉛直方向k番目の層の調節量であり、第k1層が調節される最も低い層、第k2層が調節される最も高い層である⁽¹⁰⁾。

　雲量C_mに関してNHMでは、雲水が不飽和な計算格子に移流したときに、雲水を即座に蒸発させてしまうという誤りを起こさないように、移流について、
　　　　　
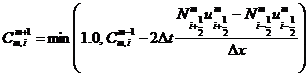
である (但し、簡便のため1次元空間について記してある)。ここで、Δxは計算格子幅、Δtは時間刻みであり、Nは、
　　　　　
　　　　　
　　　　　Otherwise,
から定まる。さらに雲水の蒸発を考慮すると、蒸発後の雲水の混合比q_c^＊と雲量C_m^＊は、
　　　　　
　　　　　
である。ここで、q_vSは飽和時の水蒸気混合比である。例外として、C_m＝1.0の場合は、
　　　　　
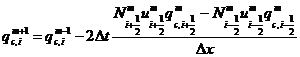
である⁽¹⁰⁾。

2.4　NHMの性能

　NHMは、MSMよりも精度が高いモデルである⁽¹⁾。運用条件は異なるが、地球シミュレータを用いてNHMを実行すると、水平規模が約2000kmの領域で、個々の対流雲スケール(数km)を再現することが可能である⁽¹²⁾。

　しかし、NHMにより現象が再現されるか否かは、親モデルであるRSMにおいて対応するモデルがきちんと表現されているかに大きく依存している⁽¹³⁾。全球モデル以外においては、一般に側面境界条件の取扱には細心の注意が必要であるが⁽⁷⁾ 、MSM・NHMともにRSMによる予測結果から側面境界条件の供給を受けている⁽¹⁴⁾。

3.　メソ数値予報に実施されたその他の改良

　本章では、近年、メソ数値予報に実施された、NHMの導入以外の改良について記す。これらは、数値予報モデルに与える初期値の改善を目的としたものである。数値予報の精度を向上させるためには、数値モデルの改良だけではなく、客観解析システムにより高精度な初期条件を求めておくことも重要である⁽¹⁴⁾。

3.1　ウインドプロファイラ

　メソモデルを効果的に運用するためには、空間・時間分解能の高い高層観測データが必要である。そこで、メソモデルの現業運用を開始する(2001年3月)にあたって新しい高層気象観測網の整備が検討され、採用・導入されたのが、観測機器「ウインドプロファイラ」(wind profiler)と、その観測網「局地的気象監視システム」:略称ウィンダスWINDAS (Wind Profiler Network and Data Acquisition System)である⁽¹⁵⁾。

　ウインドプロファイラはドップラーレーダの一種であるが、ドップラー気象レーダが雨滴や雪片などの降水粒子を媒体として風を観測するのに対し、ウインドプロファイラは空気の屈折率のゆらぎ(空間変動)によって生じる電波の散乱を受信することによって、散乱体の移動速度を通して上空の風を観測する⁽¹⁵⁾。

WINDASは2001年4月、25の観測局(ウインドプロファイラ)により完成し、2003年
6月には6観測局が追加され、観測局の数は31となった。在来の高層気象観測方法であるラジオゾンデを使った観測が18地点において6時間間隔で行われるのに対し、ウインドプロファイラは31地点において10分間隔で観測を行う。メソ数値予報につかわれるのは毎正時すなわち1時間間隔の観測値のみであるが、それでもメソ数値予報に取り込まれる高層風のデータ数が飛躍的に増加したことが分かる。また、運用面での改善も進められた⁽¹⁵⁾。http://www.weather-eye.com/wind/observe/src/profiler.html では、各観測局の観測結果を見ることができる。

3.2 4次元変分法

　数値予報モデルの精度向上には、最適な初期値を観測データから作成することが重要である⁽¹³⁾。一般に、数値予報モデルの格子点数に比べて観測データ数は不足している。また、観測データは、時間的にも空間的にも不均一に分布する。このような観測データから全ての計算格子点について初期値を求めなければならない。それには、数値予報モデルから得られる第一推定値に、統計学的推定論を用いて観測データを同化する。この方法を「データ同化」と呼ぶ。

データ同化のひとつが4次元変分法( 4-dimensional variational data assimilation, 4D-VAR )である。4次元変分法の「4次元」とは、東西・南北・高さの3次元に、時間の次元が加わっていることを意味する。4D-VARでは、東西・南北・高さの3次元に関し、解析する物理量と線形関係にない観測値もデータ同化する。時間に関しては、第一推定値の確率密度関数と、任意の時刻の観測値を数値予報モデルによって時間発展させた確率密度関数両方から導かれる推定値の確率密度関数を最大にする最尤推定値でもって、解析値を求める⁽¹⁴⁾。この解析値が、数値予報モデルの初期値に使われる。

4D-VARは、現在世界最高レベルの数値予報をしているといわれるECMWF(ヨーロッパ中期予報センター)により全球モデルの解析に導入され、大きな成果をあげた⁽¹⁶⁾。気象庁メソ数値予報には2002年3月に導入された。RSMには2003年6月に導入された。

なお、4D-VARでは、背景誤差と観測誤差はいずれもGauss分布に従うという仮定がおれる。この仮定は、上下限のある相対湿度では成り立たず、また降水量でも成り立たないことが経験的に分かっている⁽¹⁴⁾。

4. 結言

　以上、気象庁メソ数値予報の発展に関してみてきた。まとめると次のようになる。

l 計算機の発展:
　2001年3月: スパコン更新(メソ予報現業化、メソ予報水平解像度10km)。
　2006年3月(予定): スパコン更新(メソ予報水平解像度5km)。

l 数値モデルの発展:
　2004年9月: MSMからNHMにモデル変更。

l モデル初期値の改善:
　2001年4月: WINDAS使用開始(ウインドプロファイラ25局)。
　2002年3月: 4次元変分法導入。
　2003年6月: WINDAS増強(ウインドプロファイラ31局)。

メソ数値予報の精度向上に必要な改良が、ここ数年に着々と実施されたことが分かる。なお、計算機の発展について、本レポートでは陽に取り上げていないが、MSMは多くの計算機資源を必要とし、NHMはさらに多くの計算機資源を必要とする。また、4次元変分法も多くの計算機資源を必要とする。つまり、計算機の発展は、数値モデルの発展とモデル初期値の改善の大きな要素でもある。

9月のNHM導入によりメソ数値予報の精度が上がり、的確な防災気象情報が出され、気象災害による被害が低減されることを期待する。

戻る

参考文献

Webページは、すべて2004年8月7日確認した。

(1) 気象庁: 報道発表資料「防災気象情報用に新しい数値予報モデルを導入します」
(2004. 7.22) http://www.jma.go.jp/JMA_HP/jma/press/0407/22a/suchimodel.pdf

(2) 財団法人河川情報センター,気象観測最前線. PORTAL, 25, 2-9 (2003.6)
http://www.river.or.jp/kawa/mi0306/03-06_002-009.pdf

(3) 気象庁: 平成12年度版今日の気象業務 (2000)
http://www.kishou.go.jp/hakusho/2000/HN200003-1.PDF

(4) 斉藤和雄 : ＮＨＭ時間積分における重力波のスプリットと音波モードの安定化 (2002)
http://www.mri-jma.go.jp/Project/mrinpd/JMA/Saito2002spring.PDF

(5) http://www.halex.co.jp/yohoushi/co_edu1000/1_040803.htm

(6) Kazuo Saito, Teruyuki Kato, Hisaki Eito & Chiashi Muroi:
Documentation of the Meteorological Research Institute / Numerical Prediction Division Unified Nonhydrostatic Model, C-1. The governing equations (2001)
http://www.mri-jma.go.jp/Project/mrinpd/Tech.Rep/C1.htm

(7)「気象シミュレーション研究会」Webサイト内, 数値天気予報の実際と予測可能性 (2002) http://www.mets.dyndns.org/misc/nwp.html

(8) 第14章　数値予報,
http://homepage1.nifty.com/weather/yoho-note/yoho14.html

(9) 小林文明, 第22回「メソ気象研究会」の報告―メソ対流系と豪雨―, 7.練馬豪雨と東京都心周辺における積乱雲の発生特性, 天気, 51-1, 55-60 (2004. 1)
http://www.s-ws.net/tenki/pdf/51_01/p055_060.pdf

(10) Kazuo Saito, Teruyuki Kato, Hisaki Eito & Chiashi Muroi:
Documentation of the Meteorological Research Institute / Numerical Prediction Division Unified Nonhydrostatic Model, G. Physical processes and diffusion (2001)
http://www.mri-jma.go.jp/Project/mrinpd/Tech.Rep/G.htm

(11) 高村陽子 & 木田秀次, 気候変動と大陸配置について２次元放射モデルを用いた研究, 防災研究所年報, 46B, (2003)
http://www.dpri.kyoto-u.ac.jp/dat/nenpo/no46/46b0/a46b0t42.pdf

(12) 気象研究所予報研究部・企画室, メソ気象研究会開催(平成15年5月20日), 気象研究所ニュース, 平成15年第6号, 3 (2003. 6)
http://www.mri-jma.go.jp/Publish/News/MRI-news-0306.pdf　

(13) 吉崎正憲&露木義: メソ対流系の発生・発達のメカニズム解明とその予測, http://www.mri-jma.go.jp/Topics/Houkokukai2003/report2.pdf

(14) 新堀敏基, 領域解析への4次元変分法の導入について, 天気, 50-9, 21-27 (2003. 9)
http://www.s-ws.net/tenki/pdf/50_09/p021_027.pdf

(15) 加藤美雄, 阿保敏広, 小林健二, 泉川安志 & 石原正仁, 気象庁におけるウィンドプロファイラ観測業務, 天気, 50-12, 3-19 (2004. 1)
http://www.s-ws.net/tenki/pdf/50_12/p003_019.pdf

(16) 気象庁の新解析予報サイクル (2002)
http://www.d3.dion.ne.jp/~jwagtail/seirei/monolog/4dvar.html